Consider the reception of a BPSK signal in noise with unknown phase, θ, to be estimated. The two hypotheses may be expressed as

H₁ : y(t) = A cos(ω_ct + θ) + n(t), 0 ‰¤ t ‰¤ T_s

H₂ : y(t) = -A cos(ω_ct + θ) + n(t), 0 ‰¤ t ‰¤ T_s

where A is a constant and n(t) is white Gaussian noise with single-sided power spectral density N₀, and the hypotheses are equally probable [P(H₁) = P(H₂)].

(a) Using Ï•₁ and Ï•₂, as given by (11.164) as basis functions, write expressions for

f_z|θ,Hi (z₁,z₂|θ, H_i), i = 1,2

(b) Noting that

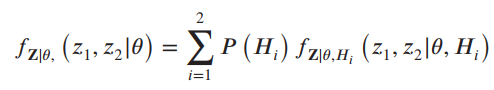
show that the ML estimator can be realized as the structure shown in Figure 11.15 by employing (11.164). Under what condition(s) is this structure approximated by a Costas loop?

Figure 11.15

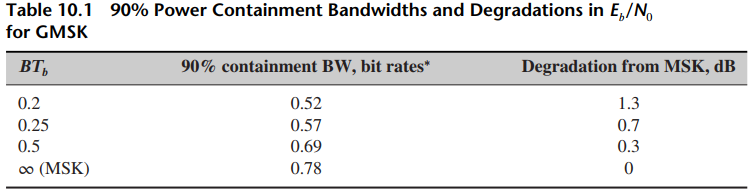
(c) Apply the Cramer-Rao inequality to find an expression for var {θ̂_ML}. Compare with the result in Table 10.1.

Transcribed Image Text:

2 S z1o. (21, Z,10) = E P (H,) fz1e.H, (z1, zl0, H,) i=1 Odt tanh ( ) K2 cos (@1 +ÔM) У() VCO х sin (@t + ÖML) „T K, Odt