Find the probability of error for non-coherent ASK, with signal set

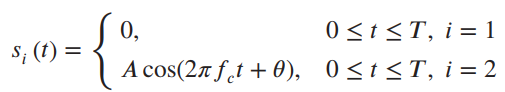
where θ is a uniformly distributed random variable in [0, 2Ï€). White Gaussian noise of two-sided power spectral density N₀ / 2 is added to this signal in the channel. The receiver is a band pass filter of bandwidth 2/T Hz centered on f_c, followed by an envelope detector, which is input to a sampler and threshold comparator. Assume that the signal, when present, is passed by the filter without distortion, and let the noise variance at the filter output be

σ²_N = N₀B_T = 2N₀ / T.

Show that the envelope detector output with signal 1 present (i.e., zero signal) is Rayleigh-distributed, and that the envelope detector output with signal 2 present is Ricean-distributed. Assuming that the threshold is set at A/2, find an expression for the probability of error. You will not be able to integrate this expression. However, by making use of the approximation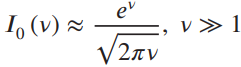

you will be able to approximate the pdf of the sampler output for large signal-to-noise ratio as Gaussian and express the probability of error in terms of a v^-1/2 in the above approximation.)

Show that the probability of error for the signal-to noise ratio large is approximately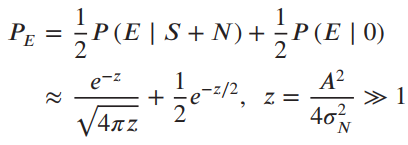 

Note that z = A² / 4σ²_N  is the average signal power- (the signal is 0 half the time) to-noise variance ratio. Plot the error probability versus the signal-to-noise ratio and compare with that for DPSK and non-coherent FSK.

Transcribed Image Text:

0, S; (t) = 0