Using the definition of a conditional pdf given by Equation (6.62) and the expressions for the marginal and joint Gaussian pdfs, show that for two jointly Gaussian random variables X and Y, the conditional density function of X given Y
has the form of a Gaussian density with conditional mean and the conditional variance given by 

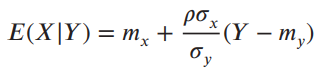
and

var(X|Y) = σ²_x (1 - p²)

respectively.

Equation (6.62)

f_XY(x,y)  = f_X(x)f_Y|X(yIx)

 = f_Y(y)f_X|Y(_X|Y)

Transcribed Image Text:

pox Е(X\Ү) — т, + *(Y – m,) бу х %3D