Develop a "parallel axis theorem" for the effective laminate stiffnesses \(A_{i j}^{\prime \prime}\), \(B_{i j}^{\prime \prime}\), and \(D_{i j}^{\prime \prime}\) associated with the \(\left(x^{\prime \prime}, z^{\prime \prime}\right)\) axes, which are parallel to the original \((x, z)\) axes, as shown in Figure 7.22. Express the new \(A_{i j}^{\prime \prime}, B_{i j}^{\prime \prime}\), and \(D_{i j}^{\prime \prime}\) in terms of the original \(A_{i j} B_{i j}\) and \(D_{i j}\) for the \((x, z)\) axes and the distance \(d\) between the parallel axes, where \(z^{\prime \prime}=z+d\).

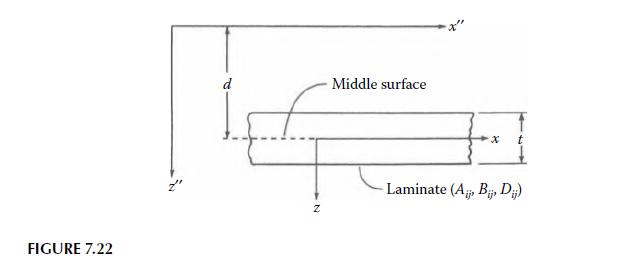
FIGURE 7.22 N d Middle surface x Z Laminate (A, B, Dij)