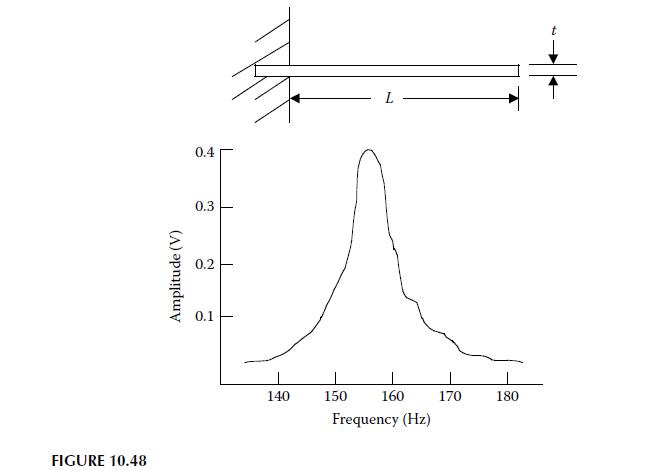
The specimen geometry and the frequency response curve for the second mode flexural vibration of a laminated composite cantilever beam specimen is shown in Figure 10.48. The specimen has length \(L=8.913\) in., width \(w=0.756 \mathrm{in}\)., thickness \(t=0.04 \mathrm{in}\)., and specific weight of \(\gamma=0.064 \mathrm{lb} / \mathrm{in} .^{3}\) (Note: \(\gamma=ho\), where \(ho=\) density and \(g=\) gravitational acceleration \(=386 \mathrm{in} . / \mathrm{s}^{2}\).) The specimen is clamped across the width as shown. Based on this data, give your best estimates for the following properties of the specimen,

(a) the flexural modulus, \(E_{\mathrm{f}}\) and

(b) the flexural loss factor, \(\eta_{\mathrm{f}}\).

Transcribed Image Text:

FIGURE 10.48 Amplitude (V) 0.4 0.3 0.2 0.1 L 140 150 160 170 180 Frequency (Hz)