5.4. In the Ehrenfest urn model (see III, Section 3.2) for molecular diffusion through a membrane, if
Question:
5.4. In the Ehrenfest urn model (see III, Section 3.2) for molecular diffusion through a membrane, if there are i particles in urn A, the probability that there will be i + 1 after one time unit is 1 - i/(2N), and the probability of i - 1 is i/(2N), where 2N is the aggregate number of particles in both urns. Following III, Section 3.2, let Y be the number of particles in urn A after the nth transition, and let X,, = Y - N. ![]() bethe change in urn composition. The probability law is
bethe change in urn composition. The probability law is
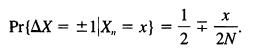
We anticipate a limiting process in which the time between transitions becomes small and the number of particles becomes large. Accordingly, let At = 1/N and measure fluctuations of a rescaled process in units of order 1/N/"N-. The definition of the rescaled process is
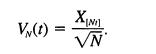
Note that in the duration t = 0 to t = 1 in the rescaled process, there are N transitions in the urns, and a unit change in the rescaled process corresponds to a fluctuation of order 1l'"N- in the urn composition. Let AV = VN(t + 1/N) - VN(t) be the displacement in the rescaled process over the time interval At = 1/N. Show that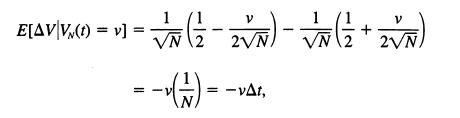
and that (AV)2 = 1/N, whence
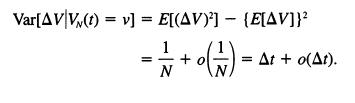
Step by Step Answer:

An Introduction To Stochastic Modeling
ISBN: 9780126848878
3rd Edition
Authors: Samuel Karlin, Howard M. Taylor






