Let (left(B_{t}ight)_{t geqslant 0}) be a (mathrm{BM}^{1}). Deduce from Theorem 12.5 the following test for upper functions
Question:
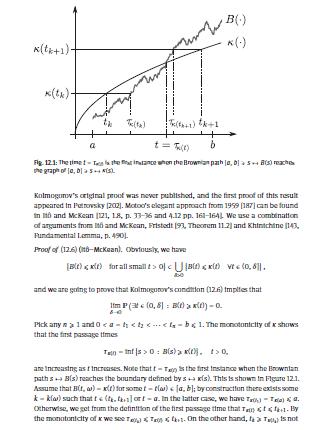
Let \(\left(B_{t}ight)_{t \geqslant 0}\) be a \(\mathrm{BM}^{1}\). Deduce from Theorem 12.5 the following test for upper functions in large time. Assume that \(\kappa \in \mathcal{C}[1, \infty)\) is a positive function such that \(\kappa(t) / t\) is decreasing and \(\kappa(t) / \sqrt{t}\) is increasing. Then \[\mathbb{P}(B(t)
Data From Theorem 12.5
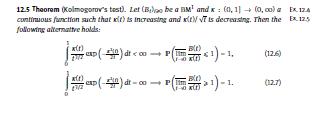

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





