Let (left(B_{t}ight)_{t geqslant 0}) be a (mathrm{BM}^{1}). Use Theorem 12.5 to show that (kappa(t)=(1+epsilon) sqrt{2 t log

Question:

Let $\left(B_{t}ight)_{t \geqslant 0}$ be a $\mathrm{BM}^{1}$. Use Theorem 12.5 to show that $\kappa(t)=(1+\epsilon) \sqrt{2 t \log |\log t|}$ is an upper function for $t ightarrow 0$.

Data From Theorem 12.5

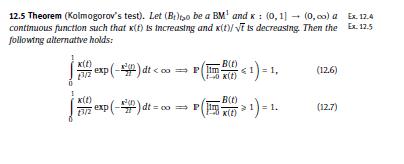
image text in transcribed

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook

ISBN: 9783110741254

3rd Edition

Authors: René L. Schilling, Björn Böttcher

See More Books

Question Posted: Mar 17, 2024 01:00 AM

See More Questions

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...
QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...
CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...
The common stock of Fido Corporation was trading at $45 per share on October 15, 2010. A year later, on October 15, 2011, it was trading at $80 per share. On this date, Fidos board of directors...
Following are two probability histograms of binomial distributions. For each, specify whether the success probability is less than, equal to, or greater than 0.5. (a) (b) p(x x) 0.35 2 0.30 0.25 0.20...
Each of the double pulleys shown has a centroidal mass moment of inertia of 0.25 kg ?? m2, an inner radius of 100 mm, and an outer radius of 150 mm. Neglecting bearing friction, determine (a) The...
If a well-behaved investment alternative's internal rate of return (IRR) is equal to MARR, which of the following statements about the other measures of worth for this alternative must be true? 1....
The City of Graftons records reflected the following budget and actual data for the General Fund for the fiscal year ended June 30, 2012. 1. Estimated revenues: Taxes (Property) ..... $3,000,000...
Show that the two drawings represent the same graph by labeling the vertices and edges of the right-hand drawing to correspond to those of the left-hand drawing. 5 el 06 Veq 5 e2 V2 ez 3 U5 (a) es 1...
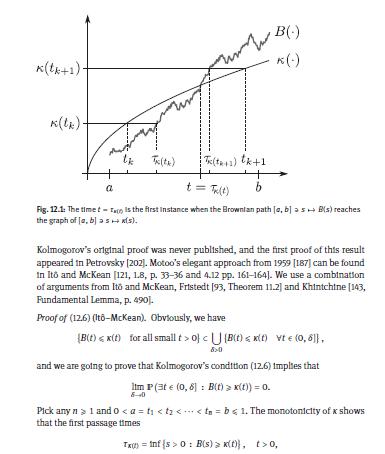
Let $\left(B_{t}ight)_{t \geqslant 0}$ be a $\mathrm{BM}^{1}$. Deduce from Theorem 12.5 the following test for upper functions in large time. Assume that $\kappa \in \mathcal{C}[1, \infty)$ is...
Show that the proof of Khinchine's LIL, Theorem 12.1, can be modified to give \[\varlimsup_{t ightarrow \infty} \frac{\sup _{s \leqslant t}|B(s)|}{\sqrt{2 t \log \log t}} \leqslant 1\] Use in Step...
The financial information below was extracted from the statement of financial position of two companies as at 30 June 20X9. Additional information 1. Both companies revalued their freehold land and...
if f ( x ) = - 7 x - 6 and g ( x ) = 8 x ^ 2 - 4 x + 3 , find g ( f ( 3 ) )
y = cos ^ ( 2 ) x - sin ^ ( 2 ) x then y ' =
As the complexity in real-world tasks and computations increases, it is vital to understand how to break up different parts of those tasks to increase efficiency. Select an issue or problem in your...
log (4x+10) - log (x+1)=3
summarize the speech in a single paragraph of around five sentences, articulate the overall point of the speech. There will be no analysis here. "Work Is Not Your Family"(opens in new window): a...
A square loop 24.0 cm on a side has a resistance of 5.20 . It is initially in a 0.665-T magnetic field, with its plane perpendicular to B, but is removed from the field in 40.0 ms. Calculate the...
At the beginning of the year, Lam Ltd. had total assets of $800,000 and total liabilities of $500,000. Use this information to answer each of the following independent questions. (a) If Lam's total...
Give an example of an intensity (t) for which the probability that no arrival will ever occur is 1/e.
A flow of arrivals N t is a non-homogeneous Poisson process with the periodical intensity (t) = | sin t|. The unit of time is a day. (a) What is the intensity of arrivals at the end and at the...
For a non-homogeneous Poisson flow of customers, the intensity (t) during the first 8 hours is increasing as 10(t/8) 2 [ending up with 10 customers/hour at the end of the period]. Find the expected...
It's grand canonical time! Let's start tutorial style: Consider a closed system with volume V, in contact with a thermal bath at temperature T and isolated from the exterior. Within this system you...
4. *Merry-go-round. Two children are playing catch on a merry-go-round that is ro- tating clockwise. A friend who is standing on the ground is pushing the merry-go- round so it is rotating faster....
1. Mat is trying to prevent Danko from reaching the ground. He is unsuccessful, however, because Danko does reach the ground 2.0 seconds after the situation shown in the diagram below. For parts a)...

Let (left(B_{t}ight)_{t geqslant 0}) be a (mathrm{BM}^{1}). Use Theorem 12.5 to show that (kappa(t)=(1+epsilon) sqrt{2 t log

Question:

12.5 Theorem (Kolmogorov's test). Let (Br)o be a BM and x: (0,1] (0,00) continuous function such that x(t) is increasing and x(t)/f is decreasing. Then the following alternative holds: Ex. 12.4 Ex. 12.5 x(t) exp(-) dt 1)=1. B(t) x(t) XI 1) = 1. (12.7)

Step by Step Answer:

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook

Students also viewed these Business questions