Show that the proof of Khinchine's LIL, Theorem 12.1, can be modified to give [varlimsup_{t ightarrow infty}
Question:
Show that the proof of Khinchine's LIL, Theorem 12.1, can be modified to give \[\varlimsup_{t ightarrow \infty} \frac{\sup _{s \leqslant t}|B(s)|}{\sqrt{2 t \log \log t}} \leqslant 1\]
Use in Step \(1^{0}\) of the proof \(\mathbb{P}\left(\sup _{s \leqslant t}|B(s)| \geqslant xight) \leqslant 4 \mathbb{P}(|B(t)| \geqslant x)\).
Data From Theorem 12.1
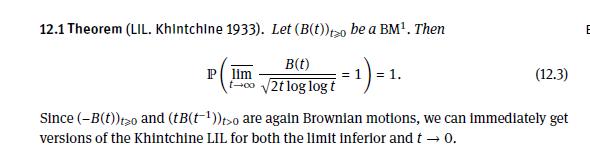
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





