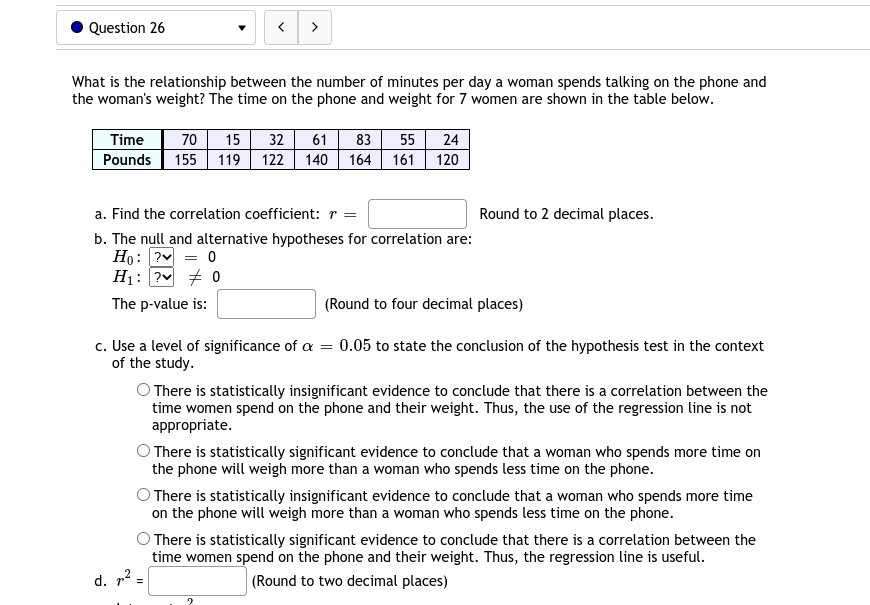
0 Question 26 v What is the relationship between the number of minutes per day a woman spends talking on the phone and the woman's weight? The time on the phone and weight for T women are shown in the table below. Time TD 15 32 b1 83 55 24 Pounds 155 119 122 140 164 161 120 a. Find the correlation coefficient: r = :| Round to 2 decimal places. b. The null and alternative hypotheses for correlation are: Hg 1 = '3 H11 # '3' The pvvalue is: |:] {Round to four decimal places} c. Use a level of significance of o: = 0.05 to state the conclusion of the hypothesis test in the context of the study. 0 There is statistically insignificant evidence to conclude that there is a correlation between the time women spend on the phone and their weight. Thus, the use of the regression line is not appropriate. Q There is statistically significant evidence to conclude that a woman who spends more time on the phone will weigh more than a woman who spends less time on the phone. Q There is statistically insignificant evidence to conclude that a woman who spends more time on the phone will weigh more than a woman who spends less time on the phone. Q There is statistically significant evidence to conclude that there is a correlation between the time women spend on the phone and their weight. Thus, the regression line is useful. d. r2 = C] {Round to two decimal places) '2! e. Interpret r2 : C) There is a large variation in women's weight, but if you only look at women with a fixed weight, this variation on average is reduced by 33955. O 33% of all women will have the average weight. C) There is a 33% chance that the regression line will be a good predictor for women's weight based on their time spent on the phone. O Given any group of women who all weight the same amount, 33% of all of these women will weigh the predicted amount. f. The equation of the linear regression line is: 3} = [:1 + :13: {Please show your answers to two decimal places} g. Use the model to predict the weight of a woman who spends 31 minutes on the phone. 1II'IIeight = C] [Please round your answer to the nearest whole number.) h. Interpret the slope of the regression line in the context of the question: 0 The slope has no practical meaning since you cannot predict a women's weight. 0 For every additional minute women spend on the phone, they tend to weigh on averge ll additional pounds. OASIEDESUP, ygoesup. i. Interpret the yvintercept in the context of the question: CI The best prediction for the weight of a woman who does not spend any time talking on the phone is 105 pounds. C) If a woman does not spend any time talking on the phone, then that woman will weigh 105 pounds. 0 The average woman's weight is predicted to be 1115. O The yvintercept has no practical meaning for this study