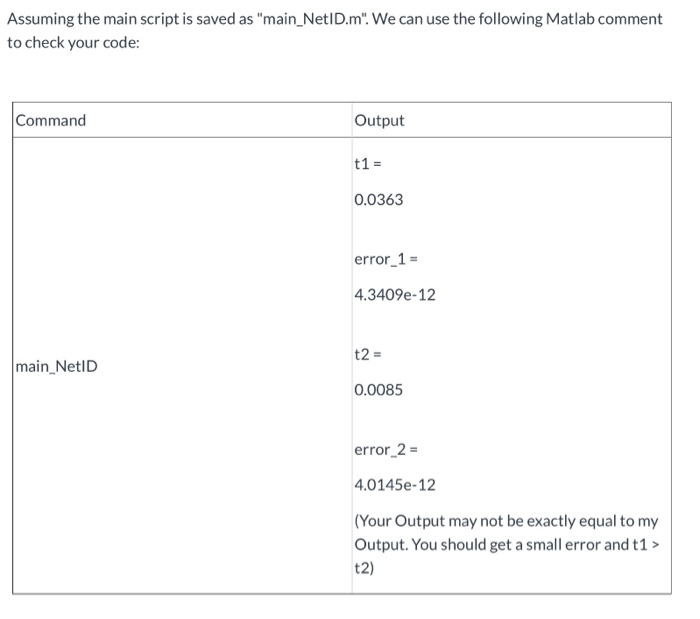
1. a MATLAB function to evaluate the Lagrange interpolating polynomial by Neville's method 2. a MATLAB function to calculate the coefficients of Lagrange interpolating polynomial, Pin Newton's form (using divided difference) 3. a MATLAB function to evaluate the interpolating polynomial in Newton's form. 4. a MATLAB script to compare the computational time of using Neville's method and using Newton's polynomial. First function: Input: x, y, X, where x is a vector consisting of Xi, y is a vector consisting of f(x;) Output: PX which is the function value of P at point X function (PX,Q] = Neville_method_NetID(x,y,X) %% Step 1: Q(:,1) = y; n = numel(x); %% Step 2: for i = 2,..., n. for j = 1, ..., -1 (Using the Neville_method to calculate Q) %% Step 4: set PX = Q(n,n); end Second function: Input: x, y, where x is a vector consisting of Xi, y is a vector consisting of f(x) Output: b where bis a vector consisting of the coefficients of the Newton's Polynomial, that is, P(x) = 61 + b2(x - 21) + ... + bn+1 =(x - Xi). function [b] = Divided_difference_NetID(x,y) %% Step 1: F(:,1) = y; %% Step 2: for i = 2,..., n for j = 1, ..., i-1 (Using the Divided_differences to calculate the coefficient) %% Step 4: set b = diag(F); end Third function: Input: b, x, X, where bis a vector consisting of the coefficients of the Newton's Polynomial and x is a vector consisting of Xi. Output: PX which is the function value of P at point X function (PX] = Newton_polynomial_NetID(b,x,X) %% Step 1: PX = b(1); S = 1; %% Step 2: for i = 2,3,..., n S = S*(X-x(i-1)) PX = PX + b(i)*s; end Main script {n = 20; m = 1000; x = (0:1:1); f = @(x) exp(x)+x; y = f(x); X = [0:1/m:1)'; PX = zeros(m+1,1); PX_N = zeros(m+1,1); tic for i = 1:m+1 PX(i) = Neville_method_NetID(x,y,X(i)); end t1(n) = toc error_1 = norm(PX-f(x)) tic [b] = Divided_difference_NetID(x,y); for i = 1:m+1 [PX_N(i)] = Newton_polynomial_NetID(b,x,x(i)); end t2(n) = toc error_2 = norm(PX_N-f(x))} Assuming the main script is saved as "main_NetID.m". We can use the following Matlab comment to check your code: Command Output t1 = 0.0363 error 1 = 4.3409e-12 t2 = main_NetID 0.0085 error 2 = 4.0145e-12 (Your Output may not be exactly equal to my Output. You should get a small error and t1 > t2)