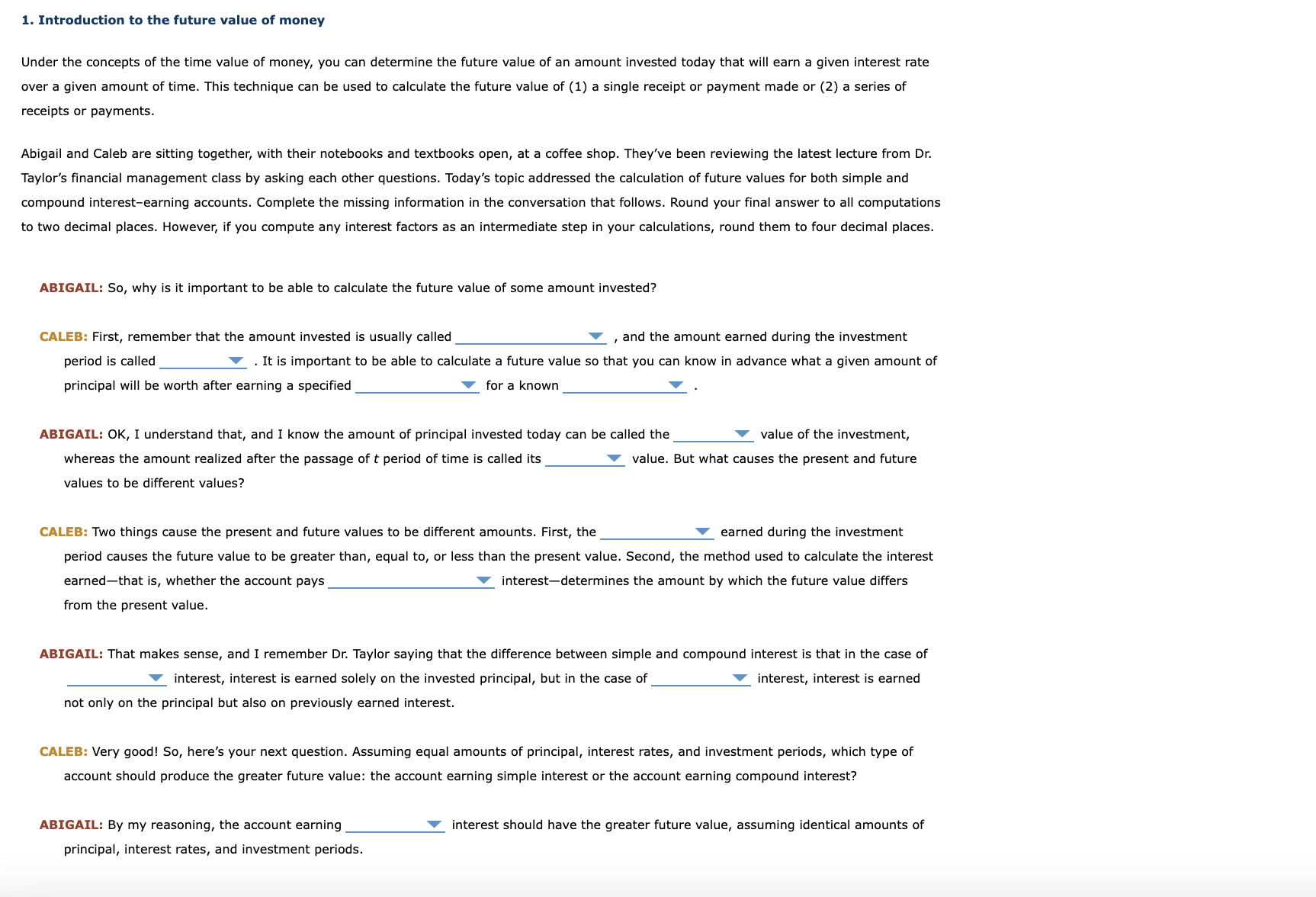
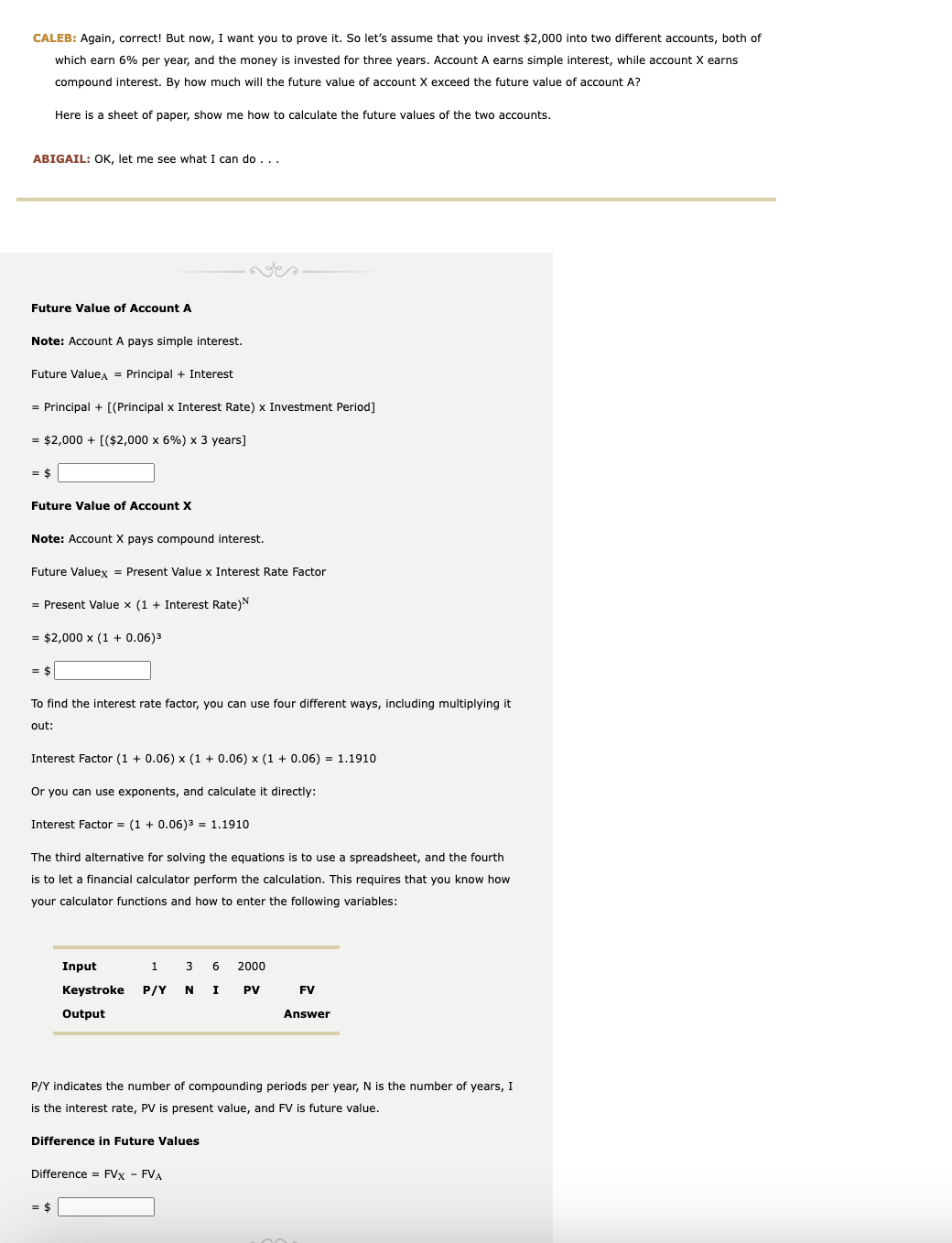
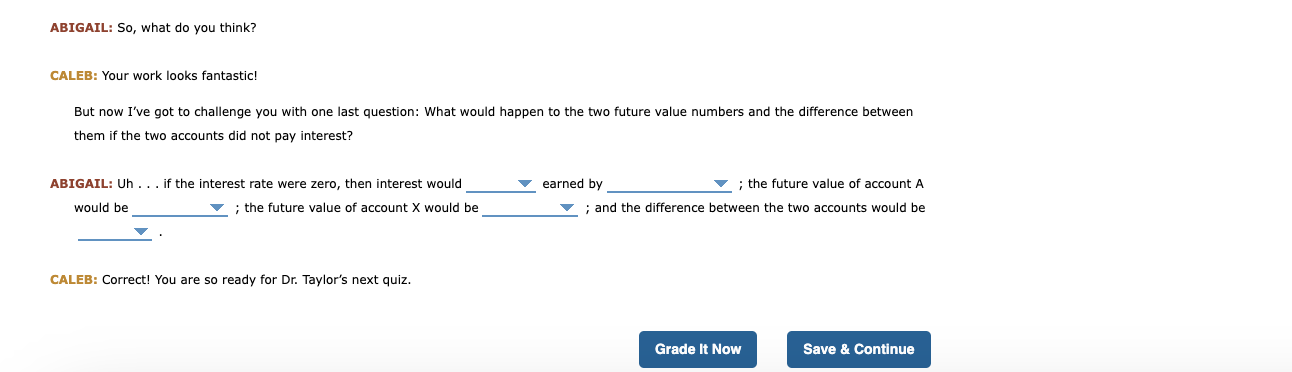1. Introduction to the future value of money Under the concepts of the time value of money, you can determine the future value of an amount invested today that will earn a given interest rate over a given amount of time. This technique can be used to calculate the future value of (1) a single receipt or payment made or (2) a series of receipts or payments. Abigail and Caleb are sitting together, with their notebooks and textbooks open, at a coffee shop. They've been reviewing the latest lecture from Dr. Taylor's financial management class by asking each other questions. Today's topic addressed the calculation of future values for bimple and compound interest-earning accounts. Complete the missing information in the conversation that follows. Round your final answer to all computations to two decimal places. However, if you compute any interest factors as an intermediate step in your calculations, round them to four decimal places. ABIGAIL: So, why is it important to be able to calculate the future value of some amount invested? CALEB: First, remember that the amount invested is usually called , and the amount earned during the investment period is called . It is important to be able to calculate a future value so that you can know in advance what a given amount of principal will be worth after earning a specified for a known ABIGAIL: OK, I understand that, and I know the amount of principal invested today can be called the value of the investment, whereas the amount realized after the passage of t period of time is called its value. But what causes the present and future values to be different values? CALEB: Two things cause the present and future values to be different amounts. First, the earned during the investment period causes the future value to be greater than, equal to, or less than the present value. Second, the method used to calest earned-that is, whether the account pays interest-determines the amount by which the future value differs from the present value. ABIGAIL: That makes sense, and I remember Dr. Taylor saying that the difference between simple and compound interest is that in the case interest, interest is earned solely on the invested principal, but in the case of interest, interest is earned not only on the principal but also on previously earned interest. CALEB: Very good! So, here's your next question. Assuming equal amounts of principal, interest rates, and investment periods, which type of account should produce the greater future value: the account earning simple interest or the account earning compound interest? ABIGAIL: By my reasoning, the account earning interest should have the greater future value, assuming identical amounts of principal, interest rates, and investment periods. CALEB: Again, correct! But now, I want you to prove it. So let's assume that you invest $2,000 into two different accounts, both of which earn 6% per year, and the money is invested for three years. Account A earns simple interest, while account X earns compound interest. By how much will the future value of account X exceed the future value of account A ? Here is a sheet of paper, show me how to calculate the future values of the two accounts. ABIGAIL: OK, let me see what I can do ... Future Value of Account A Note: Account A pays simple interest. Future Value A= Principal + Interest = Principal +[ (Principal x Interest Rate )x Investment Period ] =$2,000+[($2,0006%)3 years ] =$ Future Value of Account X Note: Account X pays compound interest. Future Value X= Present Value x Interest Rate Factor = Present Value (1+InterestRate)N =$2,000(1+0.06)3 =$ To find the interest rate factor, you can use four different ways, including multiplying it out: Interest Factor (1+0.06)(1+0.06)(1+0.06)=1.1910 Or you can use exponents, and calculate it directly: Interest Factor =(1+0.06)3=1.1910 The third alternative for solving the equations is to use a spreadsheet, and the fourth is to let a financial calculator perform the calculation. This requires that you know how your calculator functions and how to enter the following variables: P/Y indicates the number of compounding periods per year, N is the number of years, I is the interest rate, PV is present value, and FV is future value. Difference in Future Values Difference =FVXFVA ABIGAIL: So, what do you think? CALEB: Your work looks fantastic! But now I've got to challenge you with one last question: What would happen to the two future value numbers and the difference between them if the two accounts did not pay interest? ABIGAIL: Uh ... if the interest rate were zero, then interest would ialue of account A would be ; the future value of account X would be ; and the difference between the two accounts would be CALEB: Correct! You are so ready for Dr. Taylor's next quiz