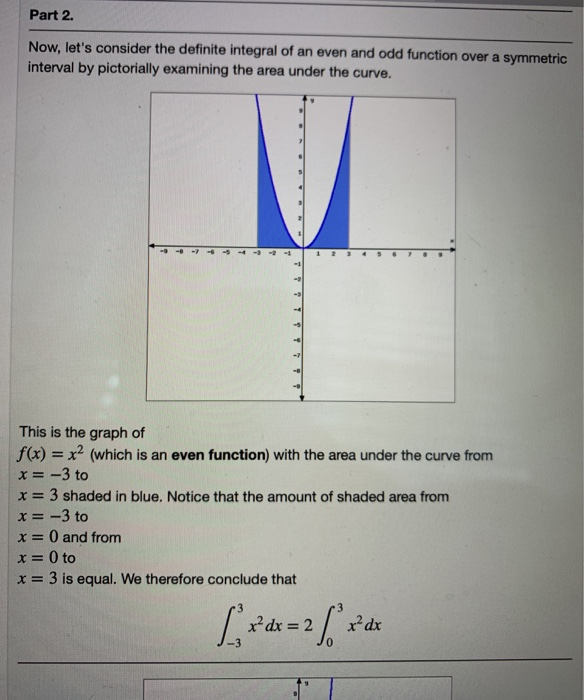
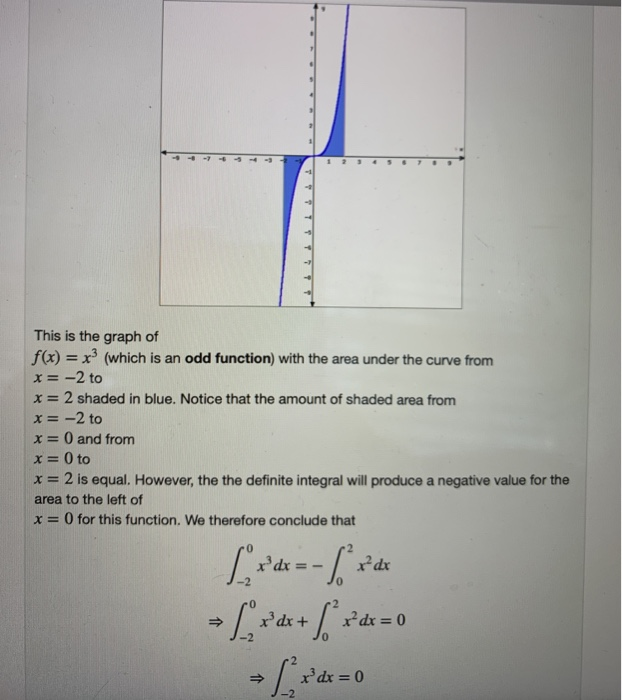
(1 point) Review the definition and properties of even and odd functions. Part1. The function f is an even function if f(-x) = f(x) for all x in the domain of f. The graph of an even function is symmetric with respect to the y-axis. The function f is an odd function if f(-x) = -f(x) for all x in the domain of f. The graph of an even function is symmetric with respect to the origin. Part 2. Now, let's consider the definite integral of an even and odd function over a symmetric interval by pictorially examining the area under the curve. Part 2. Now, let's consider the definite integral of an even and odd function over a symmetric interval by pictorially examining the area under the curve. This is the graph of f(x) = x (which is an even function) with the area under the curve from x = -3 to x = 3 shaded in blue. Notice that the amount of shaded area from x = -3 to x = 0 and from x = 0 to x = 3 is equal. We therefore conclude that [x dx = 2 [ x dx 41 1 This is the graph of f(x)= x (which is an odd function) with the area under the curve from x = -2 to x = 2 shaded in blue. Notice that the amount of shaded area from x = -2 to x = 0 and from x = 0 to x = 2 is equal. However, the the definite integral will produce a negative value for the area to the left of x = 0 for this function. We therefore conclude that == L [ x dx + xdx x dx = 0 [3dx=0 x dx = 0 Part 3. In general, S if f(x)dx= c then, if f is an even function then, [ = f(x) dx -a if f is an odd function then, a fixa f(x) dx = -a [2dx=- [ 2 dx == [ 2 dx + [ x dx = 0 x [dx=0 x dx = 0.