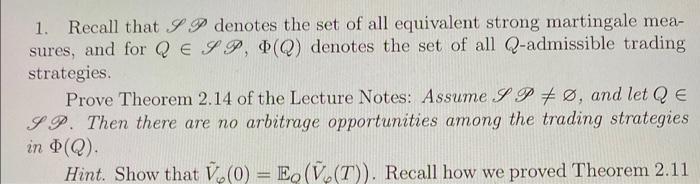1. Recall that IP denotes the set of all equivalent strong martingale mea- sures, and for Q ESP, (Q) denotes the set of all Q-admissible trading strategies Prove Theorem 2.14 of the Lecture Notes: Assume S P + , and let Qe IP. Then there are no arbitrage opportunities among the trading strategies in 0(Q). Hint. Show that (0) = E. (V (T)). Recall how we proved Theorem 2.11 Theorem 2.11. Assume + . Then there are no arbitrage opportunities among the tame trading strategies. Proof. For any tame trading strategy , under any Q EP.V (t) is a supermartingale, that is, E (V (0) F.) 0. As a result, for 0 0) = 1, (17) As a result, 101 USE EQ(V (t)) = 0 (17) Observing that PV (t) > 0) = 1. and taking into account that the probability measures P and Q are equivalent, we get Q(V (t) > 0) = 1. (18) Now, combining (17) and (18) yields V (T) = 0 Q-a.s., and so V (T) = 0 P-a.s. But this contradicts the definition of an arbitrage opportunity. In practice, the condition that the trading strategies are tame is sometimes quite restrictive. We will now see how, under certain assumptions, one does not need to assume that all trading strategies are tame. Definition 2.12. Let Q ESP be an equivalent strong martingale measure. A self- financing trading strategy is called Q-admissible if the discounted gain process &o() = ()d,(6) 0 is a Q-martingale. The class of all Q-admissible trading strategies is denoted by D(Q). Remark 2.13. We stress that the trading strategies ED(Q) are not assumed to be tame! Theorem 2.14. Assume S9+, and let Q ESP. Then there are no arbitrage opportunities among the trading strategies in 0(Q). Proof. Let ve "(Q). Since the trading strategy is self-financing, we have V (t) = V0 +G (t). Since (t) is a martingale, we therefore see that V (t) is also a martingale. But now, we can follow the lines of the proof of Theorem 2.11, where we only used that the process V (t) was a supermartingale. a a 1. Recall that IP denotes the set of all equivalent strong martingale mea- sures, and for Q ESP, (Q) denotes the set of all Q-admissible trading strategies Prove Theorem 2.14 of the Lecture Notes: Assume S P + , and let Qe IP. Then there are no arbitrage opportunities among the trading strategies in 0(Q). Hint. Show that (0) = E. (V (T)). Recall how we proved Theorem 2.11 Theorem 2.11. Assume + . Then there are no arbitrage opportunities among the tame trading strategies. Proof. For any tame trading strategy , under any Q EP.V (t) is a supermartingale, that is, E (V (0) F.) 0. As a result, for 0 0) = 1, (17) As a result, 101 USE EQ(V (t)) = 0 (17) Observing that PV (t) > 0) = 1. and taking into account that the probability measures P and Q are equivalent, we get Q(V (t) > 0) = 1. (18) Now, combining (17) and (18) yields V (T) = 0 Q-a.s., and so V (T) = 0 P-a.s. But this contradicts the definition of an arbitrage opportunity. In practice, the condition that the trading strategies are tame is sometimes quite restrictive. We will now see how, under certain assumptions, one does not need to assume that all trading strategies are tame. Definition 2.12. Let Q ESP be an equivalent strong martingale measure. A self- financing trading strategy is called Q-admissible if the discounted gain process &o() = ()d,(6) 0 is a Q-martingale. The class of all Q-admissible trading strategies is denoted by D(Q). Remark 2.13. We stress that the trading strategies ED(Q) are not assumed to be tame! Theorem 2.14. Assume S9+, and let Q ESP. Then there are no arbitrage opportunities among the trading strategies in 0(Q). Proof. Let ve "(Q). Since the trading strategy is self-financing, we have V (t) = V0 +G (t). Since (t) is a martingale, we therefore see that V (t) is also a martingale. But now, we can follow the lines of the proof of Theorem 2.11, where we only used that the process V (t) was a supermartingale. a a