1. This problem concerns the Galois field GF(2⁸) with the irreducible polynomial P(x) = x⁸+x⁴+x³+x+1. Let A(x) = x⁴+x³ and B(x) = x⁶+x³+1.

(a) How many elements in the field GF(2⁸)?

(b) What is the maximum degree of any polynomials in GF(2⁸)

(c) List all elements (i.e. polynomials) in GF(2⁸) with degree 3.

(d) Compute A(x) + B(x) mod P(x).

(e) Compute A(x) * B(x) mod P(x).

(f) Find A^-1(x) and B^-1(x) by using Table 4.2.

(g) Verify your answer in (f) by performing GF(2⁸) multiplication.

2. Your task is to compute the S-Box, i.e., the ByteSub, values for the input bytes 29, F3, and 01, where each byte is given in hexadecimal notation.

(a) First, look up the inverse using Table 4.2 to obtain values B.

(b) Now, perform the affine mapping by computing the matrix-vextor multiplication and addition.

(c) Verify your result using the S-Box Table 4.3.

(d) What is the value of S(0)?

Table 4.2

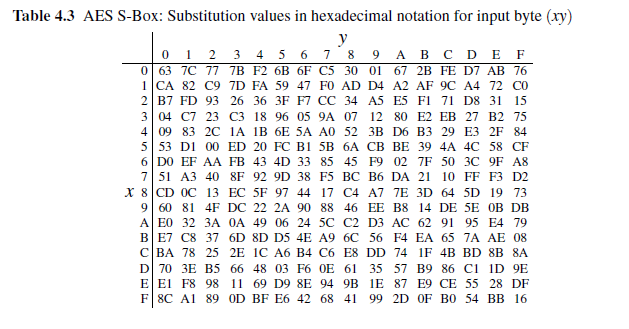
Table 4.3

Table 4.2 Multiplicative inverse table in GF(28) for bytes xy used within the AES S-Box 0123456789ABCDEF 174 B4 AA 4B 99 2B 60 5F 58 3F FD CC FF 40 EE B2 6E 55 98 15 30 44 A2 32C 45 92 6C F3 39 66 42 F2 35 20 6F 77 BB 59 19 411D FE 37 67 2D 31 F5 69 A7 64 AB 13 54 25 E9 09 51RD 5C 05 CA 4C 24 87 BF 18 3E 22 F0 51 EC 61 17 6116 5EAF D3 49 A6 36 43 F4 47 91 DF 33 93 21 3B 97 85 BA D0 06 FA 82 X8183 7E 7F 80 96 73 BE 56 9B 9E 95 D9 F7 02 B9 A4 32 6D 84 72 88 DC 9A 65 48 E7 62 B10C E0 1F EF 11 75 78 71 A5 8E 76 3D BD BC 86 57 2FA3 53 04 FC EA AD 50 F15B 23 38 34 68 46 03 8C DD 9C 7DA0 CD 1A 41 1C , 7 2 2 9 9 7 B 2 4 A 2 7 6B3C C B C 1 0 1 3 8 A 9 6 5 E6B1 9911-9926C0E1 E ES 5E628B8D8A914 D-1 0 4 B 5 C 3 A 2 C 7 C C80 E44B2E9F0DEBFF5 oo F 3 7 5 5 3 1 FFED 0 F 0 7 4 1 3 1 7 9 E D B D D D BF37553AFFCB-95C 0C5F30F698AD4530 CC16-FD0D8430DEA 9D80B2-0526347D 2F92A29D99175CD7 9-4P FFA54E70E48E7BEC 4 3 0 3 6 3 4 7 91C82849 or Y8-E8 58 ct 88-27846BA6 48D E5CFA-FB922 90D fo Y 1F929F3C6281F )7 D5C46B4357470 (2 6- B086576AE45842F3 76A6F83EB867EEC0 5-2 2 4 3 326578874 DB 2BD9-4653A854BE6 524332AB78B7DD04 953DC9068F-A568 95F244-9D8-DCC6 6B1C7A350D3F33B4 3-6 4 F 6 6 A 3 5 8 6 3 F F4F66CD886CEA6E3 DAA275F7F2EFFE68 8A5930A9732-2AD3 14E5ECE7EAC087D3 0B64, F 5 5 B 7 6 7 E 2002 693EBCBA1B 0732 178DF007B5 0123456789ABCDEF Table 4.2 Multiplicative inverse table in GF(28) for bytes xy used within the AES S-Box 0123456789ABCDEF 174 B4 AA 4B 99 2B 60 5F 58 3F FD CC FF 40 EE B2 6E 55 98 15 30 44 A2 32C 45 92 6C F3 39 66 42 F2 35 20 6F 77 BB 59 19 411D FE 37 67 2D 31 F5 69 A7 64 AB 13 54 25 E9 09 51RD 5C 05 CA 4C 24 87 BF 18 3E 22 F0 51 EC 61 17 6116 5EAF D3 49 A6 36 43 F4 47 91 DF 33 93 21 3B 97 85 BA D0 06 FA 82 X8183 7E 7F 80 96 73 BE 56 9B 9E 95 D9 F7 02 B9 A4 32 6D 84 72 88 DC 9A 65 48 E7 62 B10C E0 1F EF 11 75 78 71 A5 8E 76 3D BD BC 86 57 2FA3 53 04 FC EA AD 50 F15B 23 38 34 68 46 03 8C DD 9C 7DA0 CD 1A 41 1C , 7 2 2 9 9 7 B 2 4 A 2 7 6B3C C B C 1 0 1 3 8 A 9 6 5 E6B1 9911-9926C0E1 E ES 5E628B8D8A914 D-1 0 4 B 5 C 3 A 2 C 7 C C80 E44B2E9F0DEBFF5 oo F 3 7 5 5 3 1 FFED 0 F 0 7 4 1 3 1 7 9 E D B D D D BF37553AFFCB-95C 0C5F30F698AD4530 CC16-FD0D8430DEA 9D80B2-0526347D 2F92A29D99175CD7 9-4P FFA54E70E48E7BEC 4 3 0 3 6 3 4 7 91C82849 or Y8-E8 58 ct 88-27846BA6 48D E5CFA-FB922 90D fo Y 1F929F3C6281F )7 D5C46B4357470 (2 6- B086576AE45842F3 76A6F83EB867EEC0 5-2 2 4 3 326578874 DB 2BD9-4653A854BE6 524332AB78B7DD04 953DC9068F-A568 95F244-9D8-DCC6 6B1C7A350D3F33B4 3-6 4 F 6 6 A 3 5 8 6 3 F F4F66CD886CEA6E3 DAA275F7F2EFFE68 8A5930A9732-2AD3 14E5ECE7EAC087D3 0B64, F 5 5 B 7 6 7 E 2002 693EBCBA1B 0732 178DF007B5 0123456789ABCDEF