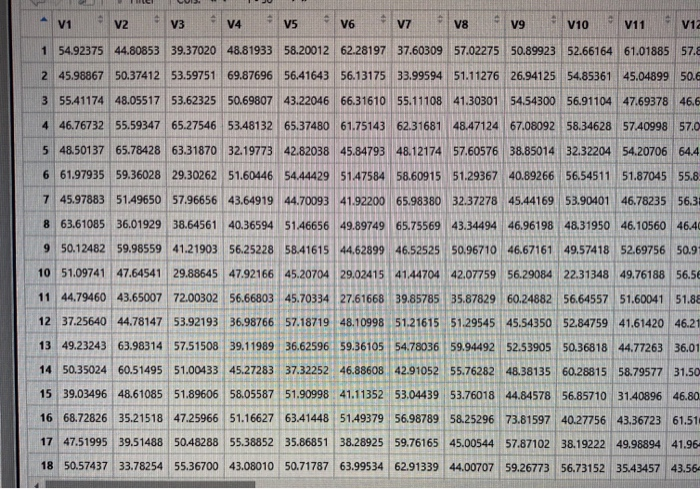
1. Use the function read.table to import the matrix stored in "bigmatrix" into R. Make sure you assign it to something for further usage. It will take a couple of seconds for R to read it. 2. Use the function dim to report the number of rows and the number of columns of the matrix. 3. Report the means of the first 10 columns. (Hint: Indexing the submatris first then use function colMeans) 4. Report the standard deviation of first 10 rows. (Hint: Indexing the submatric first then use function apply) 5. Get the 1x submatrix of the original matrix, where r is the number of columns of the original matrix which you should get from part 1, make sure what you get is still of class matrix rather than numeric. - v1v2 * v * v4 . v V6 * v * V8 V9 V10 V11 Via 1 54.92375 44.80853 39.37020 48.81933 58.20012 62.28197 37.60309 57.02275 50.89923 52.66164 61.01885 57.8 2 45.98867 50.37412 53.59751 69.87696 56.41643 56.13175 33.99594 51,11276 26.94125 54.85361 45.04899 50.6 3 55.41174 48.05517 53.62325 50.69807 43.22046 66.31610 55.11108 41.30301 54.54300 56.91104 47.69378 46.6 4 46.76732 55.59347 65.27546 53.48132 65.37480 61.75143 62.31681 48.47124 67.08092 58.34628 57.40998 57.0 5 48.50137 65.78428 6331870 32.19773 42.82038 45.84793 48.12174 57.60576 38.85014 32.32204 54.20706 64.4 6 61.97935 59.36028 29.30262 51.60446 54.44429 51.47584 58.60915 51.29367 40.89266 56.54511 51.87045 55.8 7 45.97883 51.49650 57.96656 43.64919 44.70093 41.92200 65.98380 32.37278 45.44169 53.90401 46.78235 56.3 8 63.61085 36.01929 38.64561 40.36594 51.46656 49.89749 65.75569 43.34494 46.96198 48.31950 46.10560 46.40 9 50.12482 59.98559 41.21903 56.25228 58.41615 44.62899 46.52525 50.96710 46.67161 49.57418 52.69756 50.9- 10 51.09741 47.64541 29.88645 47.92166 45.20704 29.02415 41.44704 42.07759 56.29084 2231348 49.76188 56.5 11 44.79460 43.65007 72.00302 56.66803 45.70334 27.61668 39.85785 35.87829 60.24882 56.64557 51.60041 51.88 12 37.25640 44.78147 53.92193 36.98766 57.1871948.10998 51.21615 51.29545 45.54350 52.84759 41.61420 46.21 13 49.23243 63.98314 57.51508 39.11989 36.62596 59.36105 5478036 59.94492 52.53905 50.36818 44.77263 36.01 14 50.35024 60.51495 51.00433 45.27283 37.32252 46.88608 42.91052 55.76282 48.38135 60.28815 58.79577 31.50 15 39.03496 48.61085 51.89606 58.05587 51.90998 41.11352 53.04439 53.76018 44.84578 56.85710 31.40896 46.80 16 68.72826 35.21518 47.25966 51.16627 63.41448 51.49379 56.98789 58.25296 73.81597 40.27756 43.36723 61.51 17 47.51995 39.51488 50.48288 55.38852 35.86851 38.28925 59.76165 45.00544 57.87102 38.19222 49.98894 41.96 18 50.57437 33.78254 55.36700 43.08010 50.71787 63.99534 62.91339 44.00707 59.26773 56.73152 35.43457 43.56 1. Use the function read.table to import the matrix stored in "bigmatrix" into R. Make sure you assign it to something for further usage. It will take a couple of seconds for R to read it. 2. Use the function dim to report the number of rows and the number of columns of the matrix. 3. Report the means of the first 10 columns. (Hint: Indexing the submatris first then use function colMeans) 4. Report the standard deviation of first 10 rows. (Hint: Indexing the submatric first then use function apply) 5. Get the 1x submatrix of the original matrix, where r is the number of columns of the original matrix which you should get from part 1, make sure what you get is still of class matrix rather than numeric. - v1v2 * v * v4 . v V6 * v * V8 V9 V10 V11 Via 1 54.92375 44.80853 39.37020 48.81933 58.20012 62.28197 37.60309 57.02275 50.89923 52.66164 61.01885 57.8 2 45.98867 50.37412 53.59751 69.87696 56.41643 56.13175 33.99594 51,11276 26.94125 54.85361 45.04899 50.6 3 55.41174 48.05517 53.62325 50.69807 43.22046 66.31610 55.11108 41.30301 54.54300 56.91104 47.69378 46.6 4 46.76732 55.59347 65.27546 53.48132 65.37480 61.75143 62.31681 48.47124 67.08092 58.34628 57.40998 57.0 5 48.50137 65.78428 6331870 32.19773 42.82038 45.84793 48.12174 57.60576 38.85014 32.32204 54.20706 64.4 6 61.97935 59.36028 29.30262 51.60446 54.44429 51.47584 58.60915 51.29367 40.89266 56.54511 51.87045 55.8 7 45.97883 51.49650 57.96656 43.64919 44.70093 41.92200 65.98380 32.37278 45.44169 53.90401 46.78235 56.3 8 63.61085 36.01929 38.64561 40.36594 51.46656 49.89749 65.75569 43.34494 46.96198 48.31950 46.10560 46.40 9 50.12482 59.98559 41.21903 56.25228 58.41615 44.62899 46.52525 50.96710 46.67161 49.57418 52.69756 50.9- 10 51.09741 47.64541 29.88645 47.92166 45.20704 29.02415 41.44704 42.07759 56.29084 2231348 49.76188 56.5 11 44.79460 43.65007 72.00302 56.66803 45.70334 27.61668 39.85785 35.87829 60.24882 56.64557 51.60041 51.88 12 37.25640 44.78147 53.92193 36.98766 57.1871948.10998 51.21615 51.29545 45.54350 52.84759 41.61420 46.21 13 49.23243 63.98314 57.51508 39.11989 36.62596 59.36105 5478036 59.94492 52.53905 50.36818 44.77263 36.01 14 50.35024 60.51495 51.00433 45.27283 37.32252 46.88608 42.91052 55.76282 48.38135 60.28815 58.79577 31.50 15 39.03496 48.61085 51.89606 58.05587 51.90998 41.11352 53.04439 53.76018 44.84578 56.85710 31.40896 46.80 16 68.72826 35.21518 47.25966 51.16627 63.41448 51.49379 56.98789 58.25296 73.81597 40.27756 43.36723 61.51 17 47.51995 39.51488 50.48288 55.38852 35.86851 38.28925 59.76165 45.00544 57.87102 38.19222 49.98894 41.96 18 50.57437 33.78254 55.36700 43.08010 50.71787 63.99534 62.91339 44.00707 59.26773 56.73152 35.43457 43.56