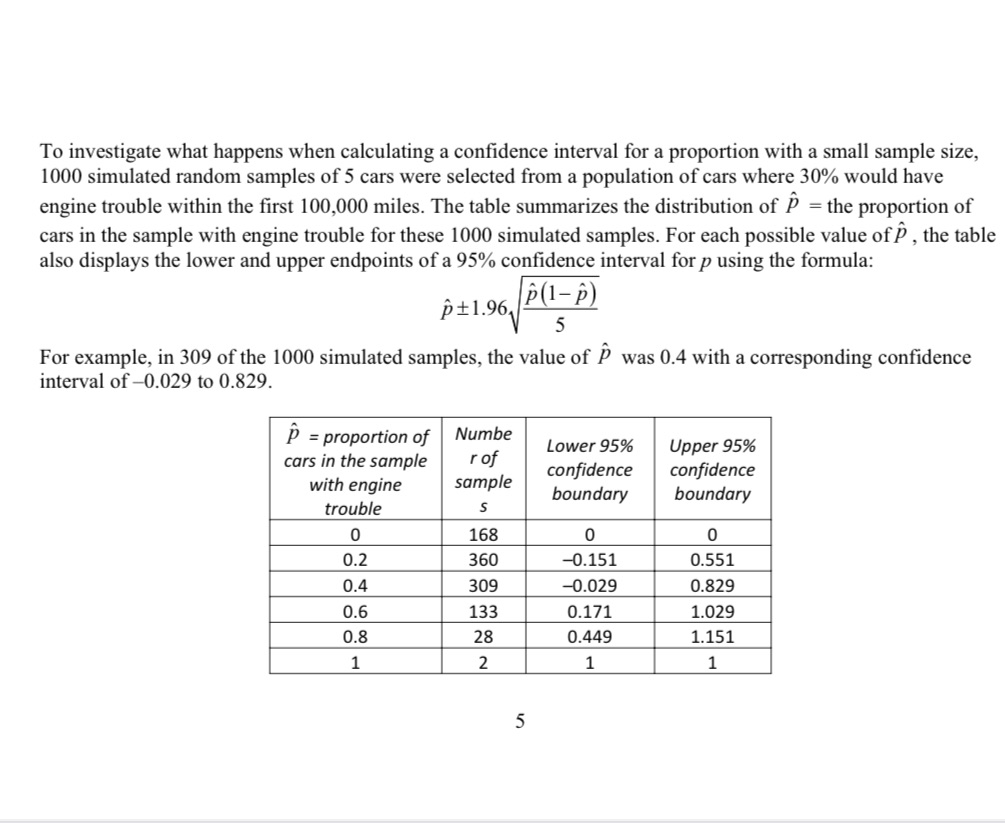
12. The manufacturer of a particular type of car claims that the engines in these cars can run for 100,000 miles without needing an oil change. To test this claim, a consumer organization plans to select a random sample of these cars and run them for 100,000 miles without an oil change, noting if any of the cars have any engine trouble during this period. Then, they will calculate a 95% confidence interval for the proportion of all cars of this type that will have engine trouble within the first 100,000 miles.(a) Explain what it means to be 95% confident in this context.(b) The consumer organization tests a random sample of 5 cars of this type and finds that 1 of the 5 cars had engine trouble within the first 100,000 miles. State and check the conditions for calculating a 95% confidence interval for the proportion of all cars of this type that would have engine trouble within the first 100,000 miles. Do not calculate the interval....after the photo below:(c) According to the simulation, how often will these 95% confidence intervals capture the true proportion of cars of this type that will have engine trouble in the first 100,000 miles? Explain how you determined your answer.(d) When the sample size is small, an alternative method for calculating a 95% confidence interval for aproportion involves adding 2 successes and 2 failures to the sample, calculating the value of p? using the original sample plus these 4 additional observations, and using the formula:p? ? 1 ? p? ? p? ?1.96(i) In the consumer organization's sample of 5 cars, 1 had engine trouble in the first 100,000 miles. What is thenvalue of p? that should be used to calculate the confidence interval for this sample, assuming that the alternativemethod is to be used?

To investigate what happens when calculating a confidence interval for a proportion with a small sample size, 1000 simulated random samples of 5 cars were selected from a population of cars where 30% would have engine trouble within the first 100,000 miles. The table summarizes the distribution of P = the proportion of cars in the sample with engine trouble for these 1000 simulated samples. For each possible value of P , the table also displays the lower and upper endpoints of a 95% confidence interval for p using the formula: p+1.96 P(1- P) 5 For example, in 309 of the 1000 simulated samples, the value of P was 0.4 with a corresponding confidence interval of -0.029 to 0.829. P = proportion of Numbe Lower 95% cars in the sample r of Upper 95% sample confidence confidence with engine trouble boundary S boundary 0 168 0 0 0.2 360 -0.151 0.551 0.4 309 -0.029 0.829 0.6 133 0.171 1.029 0.8 28 0.449 1.151 1 2 1 1 5