15.3

1.

The following estimated regression equation based on 10 observations was presented.

?=29.1210+0.5906x₁+0.4580x₂

The values of SST and SSR are6,713.125and6,224.375, respectively.

(a)

Find SSE.

SSE =

(b)

ComputeR². (Round your answer to three decimal places.)

R²=

(c)

ComputeR_a².

(Round your answer to three decimal places.)

R_a²=

(d)

Comment on the goodness of fit. (For purposes of this exercise, consider a proportion large if it is at least 0.55.)

The estimated regression equation did not provide a good fit as a large proportion of the variability inyhas been explained by the estimated regression equation.

The estimated regression equation provided a good fit as a large proportion of the variability inyhas been explained by the estimated regression equation.

The estimated regression equation provided a good fit as a small proportion of the variability inyhas been explained by the estimated regression equation.

The estimated regression equation did not provide a good fit as a small proportion of the variability inyhas been explained by the estimated regression equation.

2.

The following estimated regression equation based on 30 observations was presented.

?= 17.6 + 3.8x₁?2.3x₂+ 7.6x₃+ 2.7x₄

The values of SST and SSR are1,803and1,759, respectively.

(a)

ComputeR². (Round your answer to three decimal places.)

R²=

(b)

ComputeR_a².

(Round your answer to three decimal places.)

R_a²=

(c)

Comment on the goodness of fit. (For purposes of this exercise, consider a proportion large if it is at least 0.55.)

The estimated regression equation did not provide a good fit as a large proportion of the variability inyhas been explained by the estimated regression equation.

The estimated regression equation provided a good fit as a large proportion of the variability inyhas been explained by the estimated regression equation.

The estimated regression equation did not provide a good fit as a small proportion of the variability inyhas been explained by the estimated regression equation.

The estimated regression equation provided a good fit as a small proportion of the variability inyhas been explained by the estimated regression equation.

3.

The following estimated regression equation relating sales to inventory investment and advertising expenditures was given.

?=28+11x₁+7x₂

The data used to develop the model came from a survey of 10 stores; for those data,SST =16,000andSSR =12,640.

(a)

For the estimated regression equation given, computeR².

R²=

(b)

ComputeR_a².

(Round your answer to two decimal places.)

R_a²=

(c)

Does the model appear to explain a large amount of variability in the data? Explain. (For purposes of this exercise, consider an amount large if it is at least 55%. Round your answer to the nearest integer.)

The adjusted coefficient of determination shows that% of the variability has been explained by the two independent variables; thus, we conclude that the model

---Select---

does

does not

explain a large amount of variability.

4.

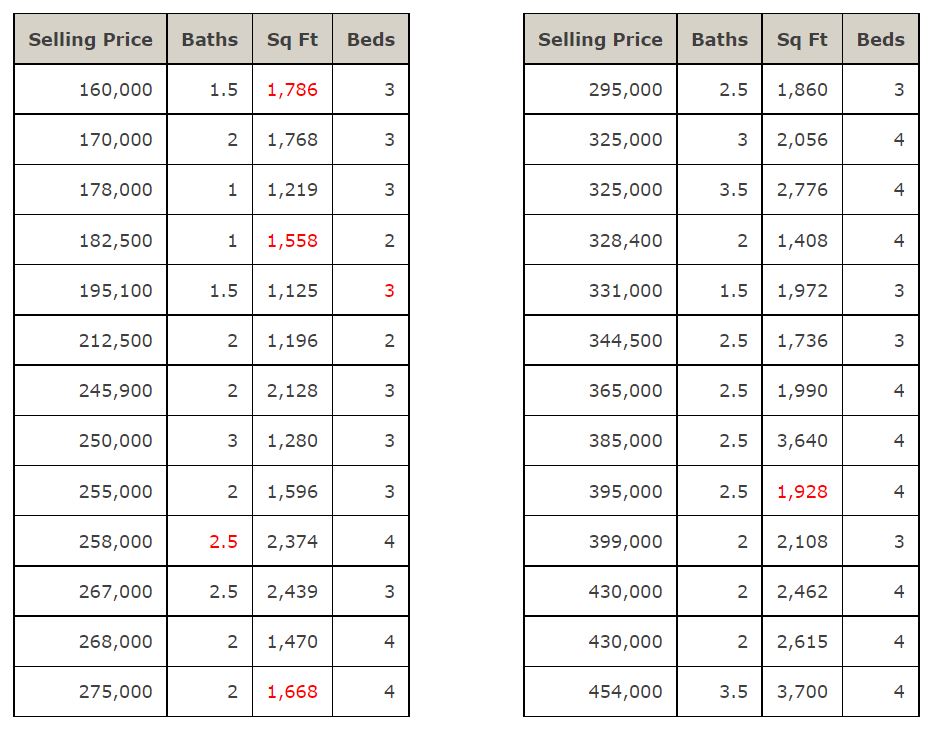
Spring is a peak time for selling houses. Suppose the data below contains the selling price, number of bathrooms, square footage, and number of bedrooms of 26 homes sold in Ft. Thomas, Kentucky, in spring 2018.

Selling Price Baths Sq Ft Beds Selling Price Baths Sq Ft Beds 160,000 1.5 1,786 3 295,000 2.5 1,860 3 170,000 2 1,768 3 325,000 3 2,056 4 178,000 1 1,219 3 325,000 3.5 2,776 4 182,500 1 1,558 2 328,400 2 1,408 4 195,100 1.5 1,125 3 331,000 1.5 1,972 3 212,500 2 1,196 2 344,500 2.5 1,736 3 245,900 2 2,128 3 365,000 2.5 1,990 4 250,000 3 1,280 3 385,000 2.5 3,640 4 255,000 2 1,596 3 395,000 2.5 1,928 4 258,000 2.5 2,374 4 399,000 2 2,108 3 267,000 2.5 2,439 3 430,000 2 2,462 4 268,000 2 1,470 4 430,000 2 2,615 4 275,000 2 1,668 4 454,000 3.5 3,700 4