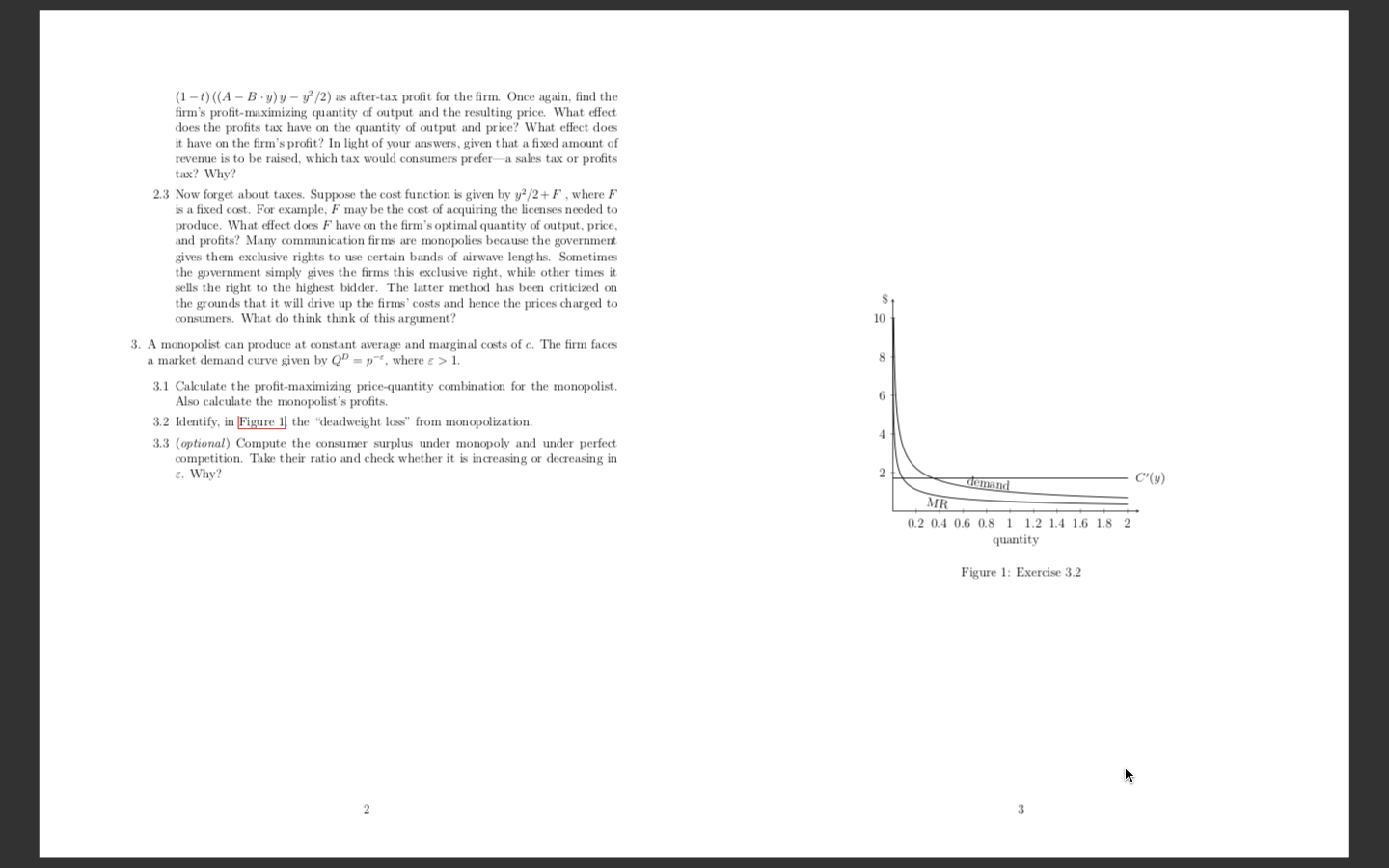
(1-t) ((A - B . y)y - y' /2) as after-tax profit for the firm. Once again, find the firm's profit-maximizing quantity of output and the resulting price. What effect does the profits tax have on the quantity of output and price? What effect does it have on the firm's profit? In light of your answers, given that a fixed amount of revenue is to be raised, which tax would consumers prefer-a sales tax or profits tax? Why? 2.3 Now forget about taxes. Suppose the cost function is given by y?/2+ F , where F is a fixed cost. For example, F may be the cost of acquiring the licenses needed to produce. What effect does F have on the firm's optimal quantity of output, price, and profits? Many communication firms are monopolies because the government gives them exclusive rights to use certain bands of airwave lengths. Sometimes the government simply gives the firms this exclusive right, while other times it sells the right to the highest bidder. The latter method has been criticized on the grounds that it will drive up the firms' costs and hence the prices charged to consumers. What do think think of this argument? 3. A monopolist can produce at constant average and marginal costs of c. The firm faces a market demand curve given by Q = p", where = > 1. 00 3.1 Calculate the profit-maximizing price-quantity combination for the monopolist. Also calculate the monopolist's profits. 6 3.2 Identify, in Figure 1 the "deadweight loss" from monopolization. 3.3 (optional) Compute the consumer surplus under monopoly and under perfect 4 competition. Take their ratio and check whether it is increasing or decreasing in E. Why? 2 demand C'(y) MR 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 quantity Figure 1: Exercise 3.2 3CAS EC 201. Intermediate Microeconomic Analysis. Problem set 8 (due on Thursday April 23, 2020) 1. First, we examine a monopolistic firm. The firm faces a market described by the (inverse) demand function p(y) = A- B . y, where p is the (maximum) price at which y units of output can be sold on the market. The firm's cost function is given by C(y) = y /2. 1.1 Find the profit-maximizing price-quantity combination for the monopolist and the corresponding profit for this firm. 1.2 Formulate your first-order condition from part 1.1 in terms of the elasticity of demand. That is, compute the demand elasticity, and use the elasticity formula to find the profit-maximizing quantity of output. 1.3 The demand is inelastic for prices below some cutoff p. What is p? Equivalently, the demand is inelastic for quantities above A/B - p/B. Show that the profit is decreasing whenever y > A/B - p/B. You have just shown that a monopolist will never choose to operate where the demand curve is inelastic. What is the intuition? 1.4 Let p' and y" be respectively the price and the quantity in 1.1, so that p* = A - B . y'. Now suppose the demand in the market shifts, so that the new (inverse) demand curve is p = A - By, with A > A and B > B, but such that it is still the case that p' = A - B . y'. Hence, if the firm does not change its quantity, its price will also not change. When is it the case that the quantity of output y" is still optimal, given this new demand curve? 2. Now suppose you must design a tax on the monopoly. 2.1 First, suppose you consider a sales tax of 10% on this market. Suppose that the firm has to pay the tax, as is typically the case with sales taxes. Hence, if the firm produces quantity y of output, the price paid by consumers is p = A - B . y, but the price received by the firm is 9p = .9A - .9B . y, where the .9 appears because the firm gets to keep only ninety percent of the purchase price, paying the remaining ten percent to the government in taxes. Find the profit maximizing quantity of output for the firm, the price paid by consumers, the price received by the firm, and the firm's profit. Explain how these answers compare to those of part 1.1. In particular, do consumers pay more as a result of the tax? Does the price received by the firm fall? Does the firm's profit fall? 2.2 Instead of a sales tax, the government considers a profits tax. Hence, if the firm chooses quantity of output y and charges price p = A - B . y, the gov- ernment collects t (py - y'/2) = t ((A - B . y) y - y'/2) in tax revenue, leaving