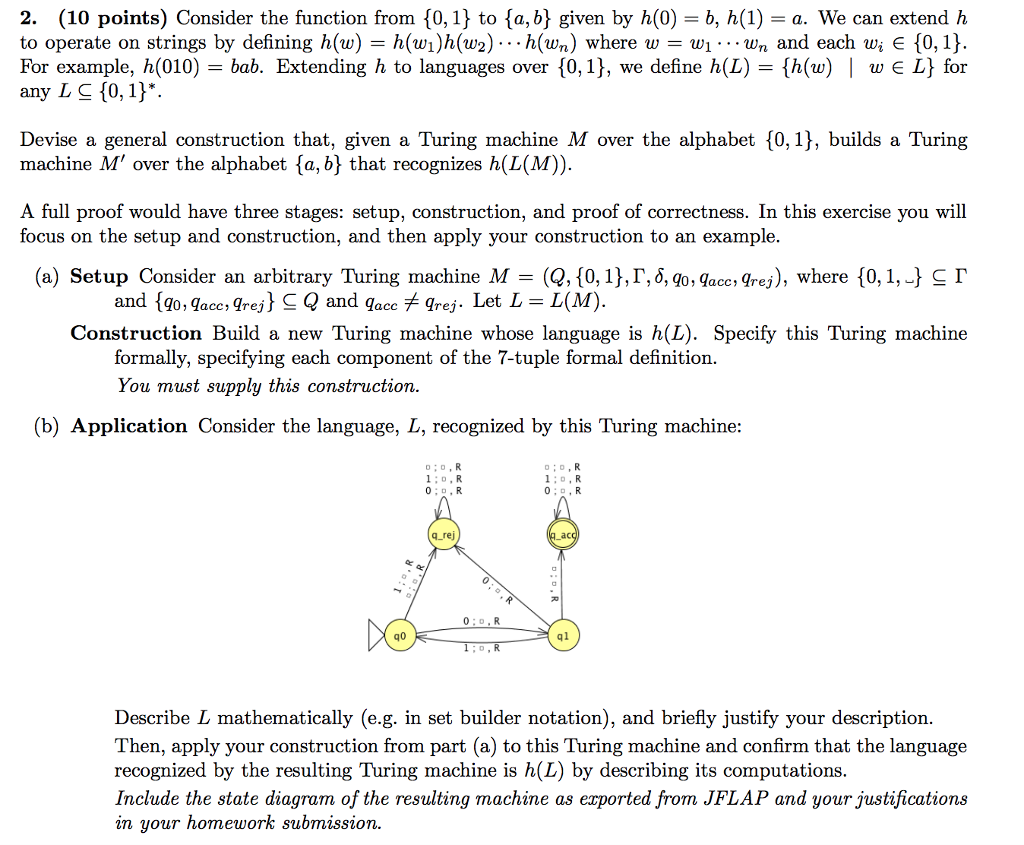
2. (10 points) Consider the function from {0,1} to {a, b} given by h(0) = b, h(1) a. We can extend h to operate on strings by defining h(w) = h(w)h(w2) h(wn) where w-w! wn and each wi e {0, 1} For example, h(010) bab. Extending h to languages over {0,1}, we define h(L) {h(w) I w E L} for any L S 10,1* Devise a general construction that, given a Turing machine M over the alphabet f0,1), builds a Turing machine M' over the alphabet {a that recognizes h(L(M)) A full proof would have three stages: setup, construction, and proof of correctness. In this exercise you will focus on the setup and construction, and then apply your construction to an example. (a) Setup Consider an arbitrary Turing machine M = (Q, {0,1),, ,,qacc ,gres), where {0, 1, . J c and 190, qacc , qrej} Q and qaccqrej. Let L = L(M) Construction Build a new Turing machine whose language is h(L). Specify this Turing machine formally, specifying each component of the 7-tuple formal definition. You must supply this construction (b) Application Consider the language, L, recognized by this Turing machine 1:o, R q.rej ac q0 Describe L mathematically (e.g. in set builder notation), and briefly justify your description. Then, apply your construction from part (a) to this Turing machine and confirm that the language recognized by the resulting Turing machine is h(L) by describing its computation:s Include the state diagram of the resulting machine as exported from JFLAP and your justifications in your homework submission. 2. (10 points) Consider the function from {0,1} to {a, b} given by h(0) = b, h(1) a. We can extend h to operate on strings by defining h(w) = h(w)h(w2) h(wn) where w-w! wn and each wi e {0, 1} For example, h(010) bab. Extending h to languages over {0,1}, we define h(L) {h(w) I w E L} for any L S 10,1* Devise a general construction that, given a Turing machine M over the alphabet f0,1), builds a Turing machine M' over the alphabet {a that recognizes h(L(M)) A full proof would have three stages: setup, construction, and proof of correctness. In this exercise you will focus on the setup and construction, and then apply your construction to an example. (a) Setup Consider an arbitrary Turing machine M = (Q, {0,1),, ,,qacc ,gres), where {0, 1, . J c and 190, qacc , qrej} Q and qaccqrej. Let L = L(M) Construction Build a new Turing machine whose language is h(L). Specify this Turing machine formally, specifying each component of the 7-tuple formal definition. You must supply this construction (b) Application Consider the language, L, recognized by this Turing machine 1:o, R q.rej ac q0 Describe L mathematically (e.g. in set builder notation), and briefly justify your description. Then, apply your construction from part (a) to this Turing machine and confirm that the language recognized by the resulting Turing machine is h(L) by describing its computation:s Include the state diagram of the resulting machine as exported from JFLAP and your justifications in your homework submission