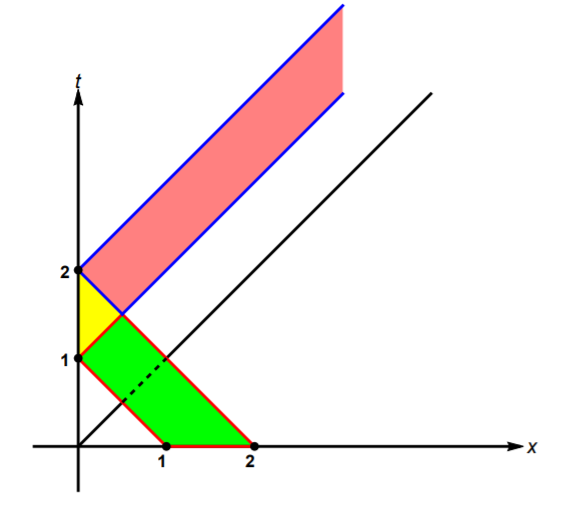
2. Consider the following initial-boundary value for the wave equation. UH Uxx = 0, x > 0, > 0 u(x,0) = f(x) = , 0 2 x) = {(x=182 *), 1sx52 . 14(x, 0) = g(x) = { 3(x 19(x = 2143 24), 15x5? 0, 05x 2 u(0,t) = 0, +20. (a) Prove that f CP (R20) and g(x) = f'(x). Hint. The notation h Ck (R20) means that function h and all its derivatives up to order k are continuous for all non-negative real numbers. (b) Consider the three regions coloured green, yellow and pink in the figure on the next page. Give a mathematical description of these regions. (c) Using the d'Alembert formula and the parallelogram rule, find the solution in the three coloured regions in the figure. Hint. In the green area, consider two cases, below and above the bisector x = t (the dashed line segment). (d) Explain why the solution is identically zero in all other regions in the first quadrant. (e) Plot the solution in the green area for t = { and in the pink area for t2 = 3. Give a physical interpretation of the solution. 2 1 2 1 N 2. Consider the following initial-boundary value for the wave equation. UH Uxx = 0, x > 0, > 0 u(x,0) = f(x) = , 0 2 x) = {(x=182 *), 1sx52 . 14(x, 0) = g(x) = { 3(x 19(x = 2143 24), 15x5? 0, 05x 2 u(0,t) = 0, +20. (a) Prove that f CP (R20) and g(x) = f'(x). Hint. The notation h Ck (R20) means that function h and all its derivatives up to order k are continuous for all non-negative real numbers. (b) Consider the three regions coloured green, yellow and pink in the figure on the next page. Give a mathematical description of these regions. (c) Using the d'Alembert formula and the parallelogram rule, find the solution in the three coloured regions in the figure. Hint. In the green area, consider two cases, below and above the bisector x = t (the dashed line segment). (d) Explain why the solution is identically zero in all other regions in the first quadrant. (e) Plot the solution in the green area for t = { and in the pink area for t2 = 3. Give a physical interpretation of the solution. 2 1 2 1 N