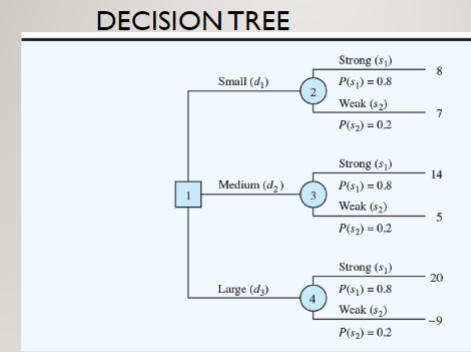
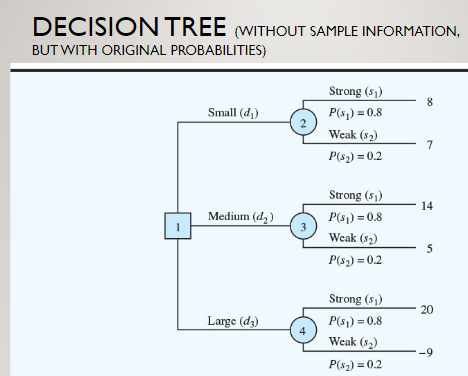
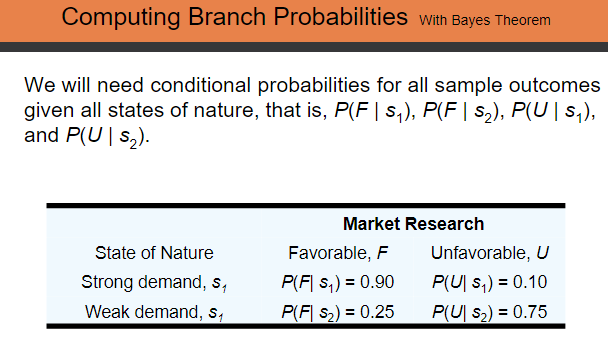
24. To save on expenses, Rona and Jerry agreed to form a carpool for traveling to and from work. Rona preferred to use the somewhat longer but more consistent Queen City Avenue. Although Jerry preferred the quicker expressway, he agreed with Rona that they should take Queen City Avenue if the expressway had a traffic jam. The following payoff table provides the one-way time estimate in minutes for traveling to or from work: Decision Alternative Queen City Avenue, d Expressway, d State of Nature Expressway Open Expressway Jammed $2 30 25 30 45 $1 Based on their experience with traffic problems, Rona and Jerry agreed on a 0.15 probabil- ity that the expressway would be jammed. In addition, they agreed that weather seemed to affect the traffic conditions on the expressway. Let C = clear 0 = overcast R = rain The following conditional probabilities apply: P(C | s) = 0.8 P(O | s) = 0.2 P(R | st) = 0.0 P(C | 52) = 0.1 P(O | 52) = 0.3 P(R | 52) = 0.6 a. Use Bayes' theorem for probability revision to compute the probability of each weather condition and the conditional probability of the expressway open, si, or jammed, 52, given each weather condition. b. Show the decision tree for this problem. 24. a. 0.695, 0.215, 0.090 0.98, 0.02 0.79, 0.21 0.00, 1.00 c. If C, Expressway If O, Expressway If R, Queen City 26.6 minutes DECISION TREE . A decision tree is a chronological representation of the decision problem. Each decision tree has two types of nodes; round nodes correspond to the states of nature while square nodes correspond to the decision alternatives. The branches leaving each round node represent the different states of nature while the branches leaving each square node represent the different decision alternatives. At the end of each limb of a tree are the payoffs attained from the series of branches making up that limb. DECISION TREE Strong (51) 8 Small (d) P(s)=0.8 2 Weak (52) 7 P(52)=0.2 Strong (51) 14 Medium (d) P(51)=0.8 Weak (32) 5 P(52)=0.2 Large (d) Strong (51) P(51)=0.8 Weak (52) 20 20 -9 P(52)=0.2 DECISION TREE (WITHOUT SAMPLE INFORMATION, BUT WITH ORIGINAL PROBABILITIES) Strong (51) 8 Small (d) P($1)=0.8 2 Weak (82) 7 P($2)=0.2 Strong (51) 14 Medium (d) P(51)=0.8 1 3 Weak ($2) 5 P(52)=0.2 Large (d3) Strong (51) P(51)=0.8 Weak ($2) 20 20 -9 P(82)=0.2 Sample Information (1 of 2) PDC has developed the following branch probabilities. If the market research study is undertaken: P(Favorable report) = P(F) = 0.77 P(Unfavorable report) = P(U) = 0.23 If the market research report is favorable: P(Strong demand | favorable report) = P(s|F) = 0.94 P(Weak demand | favorable report) = P(s|F) = 0.06 Computing Branch Probabilities with Bayes Theorem We will need conditional probabilities for all sample outcomes given all states of nature, that is, P(F | s), P(F | s), P(U | s), and P(U | S2). Market Research State of Nature Favorable, F Unfavorable, U Strong demand, s P(F| S) = 0.90 P(U| S) = 0.10 Weak demand, s P(F) $2) = 0.25 P(U| $2) = 0.75