$3\mathrm{.}10$ LAB: Natural merge sort

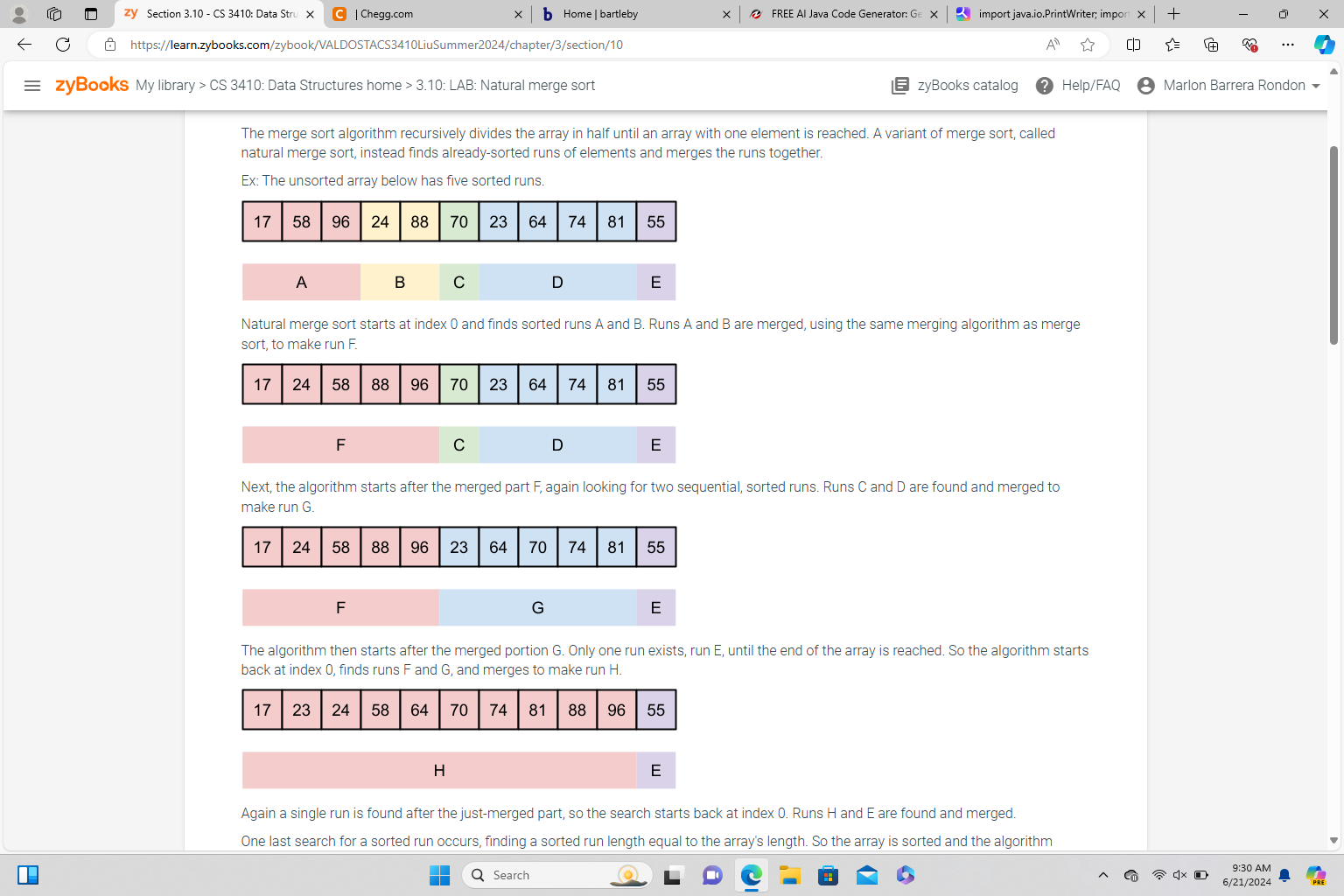
The merge sort algorithm recursively divides the array in half until an array with one element is reached. A variant of merge sort, called natural merge sort, instead finds already$-$sorted runs of elements and merges the runs together.

Ex: The unsorted array below has five sorted runs.

Array with contents $17,58,96,24,88,70,23,64,74,81,55.$ Five runs are color coded. Indices $0,1,$ and $2$ comprise run A$,$ shown in red. Indices $3$ and $4$ comprise run B$,$ shown in yellow. Index $5$ comprises run C$,$ shown in green. Indices $6,7,8,$ and $9$ comprise run D$,$ shown in blue. Index $10$ comprises run E$,$ shown in purple.

Natural merge sort starts at index $0$ and finds sorted runs A and B$.$ Runs A and B are merged, using the same merging algorithm as merge sort, to make run F$.$

Array with contents $17,24,58,88,96,70,64,74,81,55.$ Four runs are color coded. Indices $0,1,2,3$ and $4$ comprise run F$,$ shown in red. Index $5$ comprises run C$,$ shown in green. Indices $6,7,8,$ and $9$ comprise run D$,$ shown in blue. Index $10$ comprises run E$,$ shown in purple.

Next, the algorithm starts after the merged part F$,$ again looking for two sequential, sorted runs. Runs C and D are found and merged to make run G$.$

Array with contents $17,24,58,88,96,23,64,70,74,81,55.$ Three runs are color coded. Indices $0,1,2,3$ and $4$ comprise run F$,$ shown in red. Indices $5,6,7,8,$ and $9$ comprise run G$,$ shown in blue. Index $10$ comprises run E$,$ shown in purple.

The algorithm then starts after the merged portion G$.$ Only one run exists, run E$,$ until the end of the array is reached. So the algorithm starts back at index $0,$ finds runs F and G$,$ and merges to make run H$.$

Array with contents $17,23,24,58,64,70,74,81,88,96,55.$ Two runs are color coded. Indices $0,1,2,3,4,5,6,7,8,$ and $9$ comprise run H$,$ shown in red. Index $10$ comprises run E$,$ shown in purple.

Again a single run is found after the just$-$merged part, so the search starts back at index $0.$ Runs H and E are found and merged.

One last search for a sorted run occurs, finding a sorted run length equal to the array's length. So the array is sorted and the algorithm terminates.

Sorted array with contents $17,23,24,55,58,64,70,74,81,88,96.$

Step $1$: Implement the getSortedRunLength$()$ method

Implement the getSortedRunLength$()$ method in NaturalMergeSorter.java. Access NaturalMergeSorter.java by clicking on the orange arrow next to NaturalMerge.java at the top of the coding window.

getSortedRunLength$()$ has three parameters:

array: a reference to an array of integers,

arrayLength: an integer for the array's length, and

startIndex: an integer for the run's starting index.

The method returns the number of array elements sorted in ascending order, starting at startIndex and ending either at the end of the sorted run, or the end of the array, whichever comes first. The method returns $0$ if startIndex is out of bounds.

File NaturalMerge.java has several test cases for getSortedRunLength$()$ that can be run by clicking the "Run program" button. One test case also exists for naturalMergeSort$(),$ but that can be ignored until step two is completed.

The program's output does not affect grading.

Submit for grading to ensure that the getSortedRunLength$()$ unit tests pass before proceeding.

Step $2$: Implement the naturalMergeSort$()$ method

Implement the naturalMergeSort$()$ method in NaturalMergeSorter.java. naturalMergeSort$()$ must:

Start at index i$=0$

Get the length of the first sorted run, starting at i

Return if the first run's length equals the array length

If the first run ends at the array's end, reassign i$=0$ and repeat step $2$

Get the length of the second sorted run, starting immediately after the first

Merge the two runs with the provided merge$()$ method

Reassign i with the first index after the second run, or $0$ if the second run ends at the array's end

Go to step $2$The merge sort algorithm recursively divides the array in half until an array with one element is reached. A variant of merge sort, called

natural merge sort, instead finds already$-$sorted runs of elements and merges the runs together.

Ex: The unsorted array below has five sorted runs.

A

B

C

D

Natural merge sort starts at index $0$ and finds sorted runs A and $B.$ Runs A and $B$ are merged, using the same merging algorithm as merge

sort, to make run $F.$

F

C

D

Next, the algorithm starts after the merged part F$,$ again looking for two sequential, sorted runs. Runs $C$ and $D$ are found and merged to

make run $G.$

$F$

G

The algorithm then starts after the merged portion G$.$ Only one run exists, run E$,$ until the end of the array is reached. So the algorithm starts

back at index $0,$ finds runs $F$ and $G,$ and merges to make run