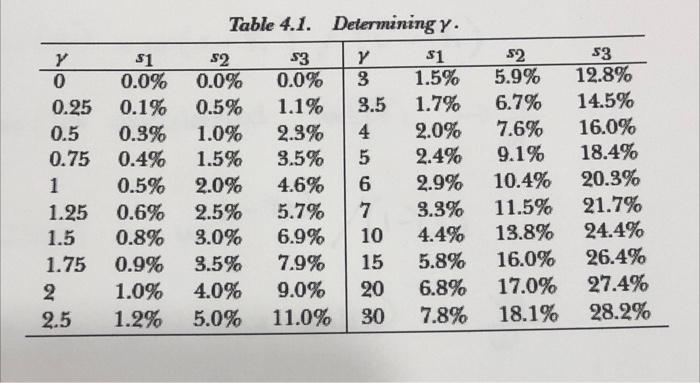
3. (35 points) Now consider a variation of the binary lottery we saw before. Instead of losing $10 with some probability, the game is now that you have a 50% probability of losing 10% of your wealth. For the beggar this amounts to something like 50 cents; for the millionaire it would be $100,000. Who requires a larger payment up front, in percentage of his wealth, to enter this gamble? This is not an easy question. Suppose the millionaire requires $70,000, which is not totally absurd, and the beggar requires 30 cents, which again may make sense. Then the millionaire requires a larger payment in percentage of his wealth than the beggar. In that case, we say that the millionaire is more relatively risk averse than the beggar. The coefficient that measures this is the coefficient of relative risk aversion, defined as R(w) := w* A(w) where A(w) denotes the coefficient of absolute risk aversion. If R is independent of wealth, we say that the utility function is in the constant relative risk aversion, or CRRA, class. Similarly, some utilities exhibit increasing (IRRA) or decreasing (DRRA) relative risk aversion. Complete the questionnaire below and determine the degree of your risk aversion. Box 4.6 Determine your preferences 1. How much do you consume every year on average (in money units)? y = 2. Compute 10%, 20%, 30% of your yearly consumption. For en- hanced concreteness, think of an item that is worth that much. 71:= y. 10% = item item 72=y-20%= 73:= y.30% = item 3. Suppose you are subject to a lottery. This lottery takes place only once and the odds are 50-50. If you win the lottery, you will receive a tax rebate of r every year from now on. If you lose the lottery you will be subject to an additional tax every year. This gives rise to three lotteries, every year from now on, depending on r: (y-r) or L: 50-50 chance of consuming. L2:50-50 chance of consuming_ L3:50-50 chance of consuming (y-2) or (y-73) or 4. Suppose you can avoid this risk and exchange it for some safe amount of consumption. What safe level of yearly consumption feels equivalent to the risky situation shown above? Try to make this feel as real as possible. Think of a risk-free consumption level that you would clearly prefer relative to the risky lottery. Then think of a consumption level that would clearly make you feel worse, so that you would rather be subject to the uncertainty of the lottery. Then narrow the boundaries. Try to determine the consumption level at which your decision switches. The safe consumption level of (=: c1) feels equivalent to L. The safe consumption level of (=: c) feels equivalent to L2. The safe consumption level of (=: c3) feels equivalent to L3. 5. Compute the implicit risk premia by subtracting c, c, c3 from your initial consumption y, then dividing these by y. Express the results in percentage points: 1 51:= (y-c1)/y = $2:= (y-c2)/y = 53:= (y-c3)/y= 6. Look up the corresponding ys from Table 4.1, y (1)= y(52) = Note: An electronic version of this experiment may be downloaded from the book's website. % % % 1 (x+r) -(y + m) (y+73) y (53)= Y 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.5 Table 4.1. Determining y. $3 $1 $2 $1 0.0% 0.0% 1.5% 5.9% 0.1% 1.1% 3.5 1.7% 6.7% 0.3% 1.0% 2.3% 4 2.0% 7.6% 0.4% 1.5% 3.5% 5 2.4% 9.1% 0.5% 2.0% 4.6% 6 2.9% 10.4% 0.6% 2.5% 5.7% 7 3.3% 11.5% 0.8% 3.0% 6.9% 10 4.4% 13.8% 0.9% 3.5% 7.9% 15 5.8% 16.0% 1.0% 4.0% 9.0% 20 6.8% 17.0% 1.2% 5.0% 11.0% 30 7.8% 18.1% $2 0.0% 0.5% Y 3 $3 12.8% 14.5% 16.0% 18.4% 20.3% 21.7% 24.4% 26.4% 27.4% 28.2% 3. (35 points) Now consider a variation of the binary lottery we saw before. Instead of losing $10 with some probability, the game is now that you have a 50% probability of losing 10% of your wealth. For the beggar this amounts to something like 50 cents; for the millionaire it would be $100,000. Who requires a larger payment up front, in percentage of his wealth, to enter this gamble? This is not an easy question. Suppose the millionaire requires $70,000, which is not totally absurd, and the beggar requires 30 cents, which again may make sense. Then the millionaire requires a larger payment in percentage of his wealth than the beggar. In that case, we say that the millionaire is more relatively risk averse than the beggar. The coefficient that measures this is the coefficient of relative risk aversion, defined as R(w) := w* A(w) where A(w) denotes the coefficient of absolute risk aversion. If R is independent of wealth, we say that the utility function is in the constant relative risk aversion, or CRRA, class. Similarly, some utilities exhibit increasing (IRRA) or decreasing (DRRA) relative risk aversion. Complete the questionnaire below and determine the degree of your risk aversion. Box 4.6 Determine your preferences 1. How much do you consume every year on average (in money units)? y = 2. Compute 10%, 20%, 30% of your yearly consumption. For en- hanced concreteness, think of an item that is worth that much. 71:= y. 10% = item item 72=y-20%= 73:= y.30% = item 3. Suppose you are subject to a lottery. This lottery takes place only once and the odds are 50-50. If you win the lottery, you will receive a tax rebate of r every year from now on. If you lose the lottery you will be subject to an additional tax every year. This gives rise to three lotteries, every year from now on, depending on r: (y-r) or L: 50-50 chance of consuming. L2:50-50 chance of consuming_ L3:50-50 chance of consuming (y-2) or (y-73) or 4. Suppose you can avoid this risk and exchange it for some safe amount of consumption. What safe level of yearly consumption feels equivalent to the risky situation shown above? Try to make this feel as real as possible. Think of a risk-free consumption level that you would clearly prefer relative to the risky lottery. Then think of a consumption level that would clearly make you feel worse, so that you would rather be subject to the uncertainty of the lottery. Then narrow the boundaries. Try to determine the consumption level at which your decision switches. The safe consumption level of (=: c1) feels equivalent to L. The safe consumption level of (=: c) feels equivalent to L2. The safe consumption level of (=: c3) feels equivalent to L3. 5. Compute the implicit risk premia by subtracting c, c, c3 from your initial consumption y, then dividing these by y. Express the results in percentage points: 1 51:= (y-c1)/y = $2:= (y-c2)/y = 53:= (y-c3)/y= 6. Look up the corresponding ys from Table 4.1, y (1)= y(52) = Note: An electronic version of this experiment may be downloaded from the book's website. % % % 1 (x+r) -(y + m) (y+73) y (53)= Y 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.5 Table 4.1. Determining y. $3 $1 $2 $1 0.0% 0.0% 1.5% 5.9% 0.1% 1.1% 3.5 1.7% 6.7% 0.3% 1.0% 2.3% 4 2.0% 7.6% 0.4% 1.5% 3.5% 5 2.4% 9.1% 0.5% 2.0% 4.6% 6 2.9% 10.4% 0.6% 2.5% 5.7% 7 3.3% 11.5% 0.8% 3.0% 6.9% 10 4.4% 13.8% 0.9% 3.5% 7.9% 15 5.8% 16.0% 1.0% 4.0% 9.0% 20 6.8% 17.0% 1.2% 5.0% 11.0% 30 7.8% 18.1% $2 0.0% 0.5% Y 3 $3 12.8% 14.5% 16.0% 18.4% 20.3% 21.7% 24.4% 26.4% 27.4% 28.2%