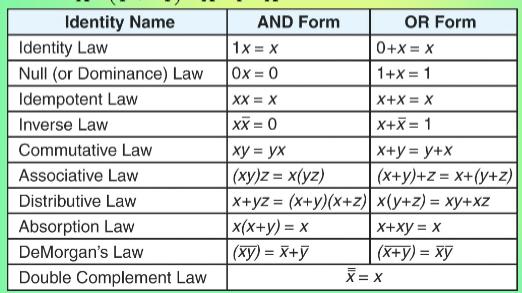
3) Given the following two expressions, prove that they are equivalent by * (X * Z + Z) * (X + Y) (Y * Z) + X = (W + X) + (X (Y+Z)) a. Simplifying them both to the same expression (you will likely have to simplify both until reach the same expression for both). Hint: do not use the distributive property on the RHS term in X * (Y + Z) until you apply DeMorgan's law. b. Derive both expressions' truth tables which should have the same results Identity Name AND Form 1x=x OR Form 0+x=x Identity Law Null (or Dominance) Law 0x = 0 Idempotent Law XX = X Inverse Law XX=0 Commutative Law Associative Law Distributive Law Absorption Law DeMorgan's Law Double Complement Law 1+x=1 X+X = X x+x=1 x+y= y+x xy = yx (xy)z = x(yz) x+yz= (x+y)(x+2) (x+y)+z=x+(y+z) x(y+z) = xy+xz x+xy = x |x(x+y)=x (xy) = x+y (x+y)=xy x = x