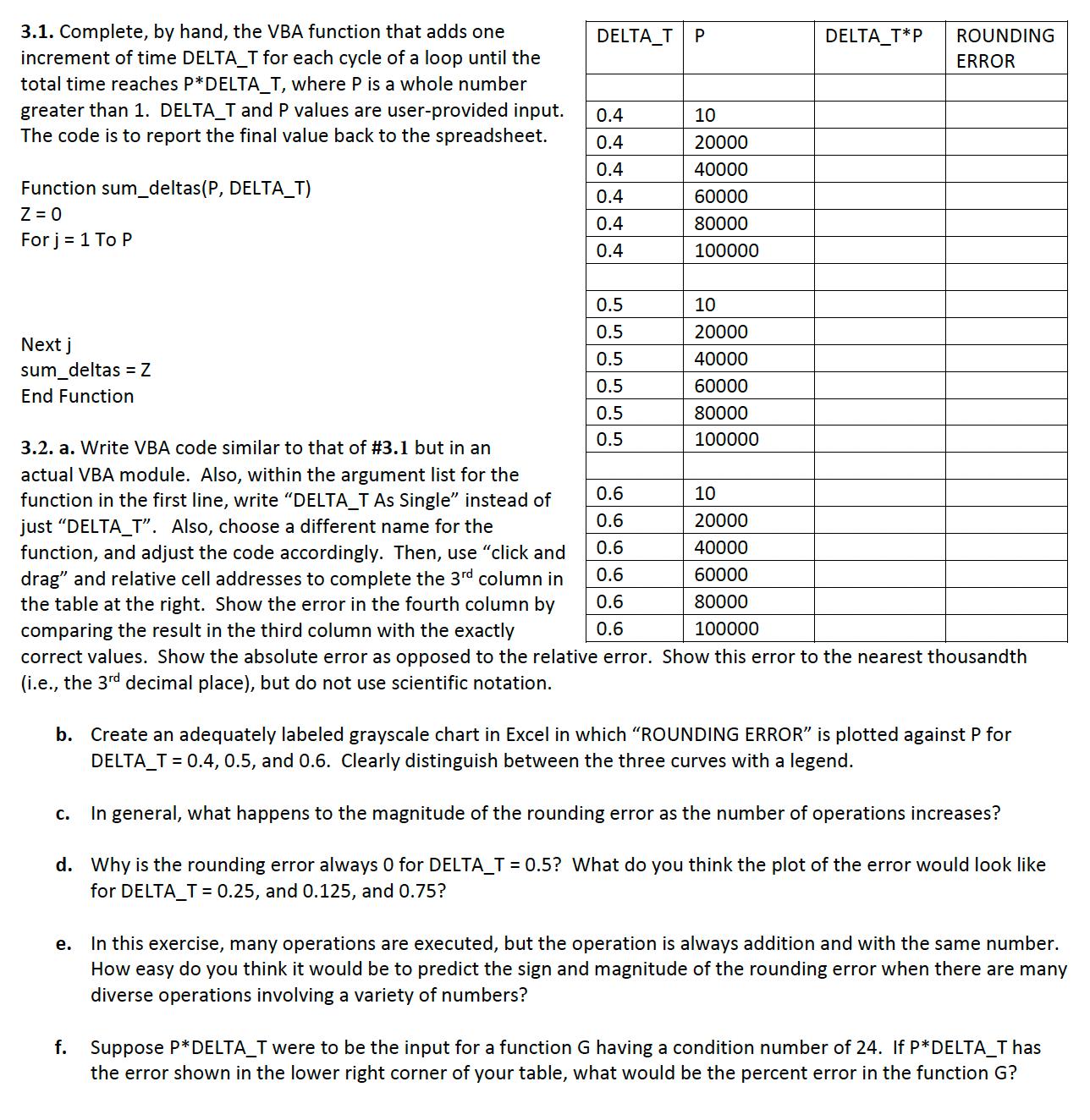
3.1. Complete, by hand, the VBA function that adds one increment of time DELTA_T for each cycle of a loop until the total time reaches P*DELTA_T, where P is a whole number greater than 1. DELTA_T and P values are user-provided input. The code is to report the final value back to the spreadsheet. Function sum_deltas(P, DELTA_T) Z = O For j = 1 To P DELTA_T P DELTA_T*P ROUNDING ERROR 0.4 10 0.4 20000 0.4 40000 0.4 60000 0.4 80000 0.4 100000 Next j sum deltas = Z End Function ollolol 0.5 10 0.5 20000 0.5 40000 0.5 60000 0.5 80000 0.5 100000 0.6 10 0.6 20000 0.6 40000 0.6 60000 0.6 80000 0.6 100000 3.2. a. Write VBA code similar to that of #3.1 but in an actual VBA module. Also, within the argument list for the function in the first line, write "DELTA_T As Single" instead of just "DELTA_T". Also, choose a different name for the function, and adjust the code accordingly. Then, use "click and drag" and relative cell addresses to complete the 3rd column in the table at the right. Show the error in the fourth column by comparing the result in the third column with the exactly correct values. Show the absolute error as opposed to the relative error. Show this error to the nearest thousandth (i.e., the 3rd decimal place), but do not use scientific notation. b. Create an adequately labeled grayscale chart in Excel in which "ROUNDING ERROR" is plotted against P for DELTA T = 0.4, 0.5, and 0.6. Clearly distinguish between the three curves with a legend. C. In general, what happens to the magnitude of the rounding error as the number of operations increases? d. Why is the rounding error always 0 for DELTA_T = 0.5? What do you think the plot of the error would look like for DELTA T = 0.25, and 0.125, and 0.75? e. In this exercise, many operations are executed, but the operation is always addition and with the same number. How easy do you think it would be to predict the sign and magnitude of the rounding error when there are many diverse operations involving a variety of numbers? f. Suppose P*DELTA_T were to be the input for a function G having a condition number of 24. If P*DELTA_T has the error shown in the lower right corner of your table, what would be the percent error in the function G?