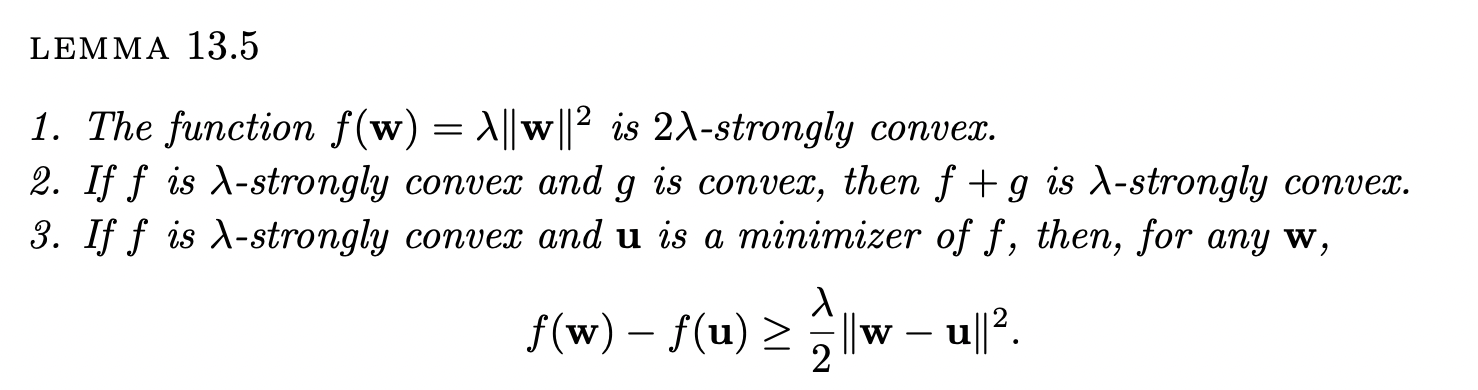
4. Strong Convexity with Respect to General Norms: Throughout the section we used the 2 norm. In this exercise we generalize some of the results to general norms. Let |||| be some arbitrary norm, and let f be a strongly convex function with respect to this norm (see Definition 13.4). 1. Show that items 2-3 of Lemma 13.5 hold for every norm. 2. (*) Give an example of a norm for which item 1 of Lemma 13.5 does not hold. DEFINITION 13.4 (Strongly Convex Functions) A function f is \-strongly con- vex if for all w, u and a (0, 1) we have - (aw + (1 a)u) a(w) + (1 a) f(u) a(1 a)||w u|. - 2 - LEMMA 13.5 1. The function f(w) = \||w|| is 2-strongly convex. 2. If f is -strongly convex and g is convex, then f+g is \-strongly convex. 3. If f is X-strongly convex and u is a minimizer of f, then, for any w, - (w) f(u) ||w u||. - 2