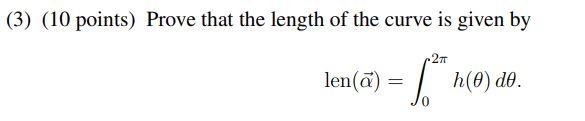
(40 points) Suppose that (t): R + R2 is a convex curve with the origin inside the curve. There is exactly one tangent line to a given in implict form by (, (cos 6, sin )) = h(0) > 0 for each angle 0. = h (0) (0) h(e) e Definition. We call h(0) the support function of the curve (0). (1) (10 points) Prove that the curve (0) can be expressed in terms of h() as a(0) = (h(0) cos 0 - h'(O) sin 0, h(0) sin + h'() cos 6). using the hypothesis that (7, (cos , sin 8)) = h(0) is the tangent line to (). (2) (10 points) Prove that the curvature of the curve at (0) is given by K+(0) = 1 h(0) +h"(0) Hint: Since the curve (0) is not parametrized by arclength, you'll need the general formula for ku(t) for non-arclength parametrized curves (3) (10 points) Prove that the length of the curve is given by len(a) 1,"n() ao. (40 points) Suppose that (t): R + R2 is a convex curve with the origin inside the curve. There is exactly one tangent line to a given in implict form by (, (cos 6, sin )) = h(0) > 0 for each angle 0. = h (0) (0) h(e) e Definition. We call h(0) the support function of the curve (0). (1) (10 points) Prove that the curve (0) can be expressed in terms of h() as a(0) = (h(0) cos 0 - h'(O) sin 0, h(0) sin + h'() cos 6). using the hypothesis that (7, (cos , sin 8)) = h(0) is the tangent line to (). (2) (10 points) Prove that the curvature of the curve at (0) is given by K+(0) = 1 h(0) +h"(0) Hint: Since the curve (0) is not parametrized by arclength, you'll need the general formula for ku(t) for non-arclength parametrized curves (3) (10 points) Prove that the length of the curve is given by len(a) 1,"n() ao