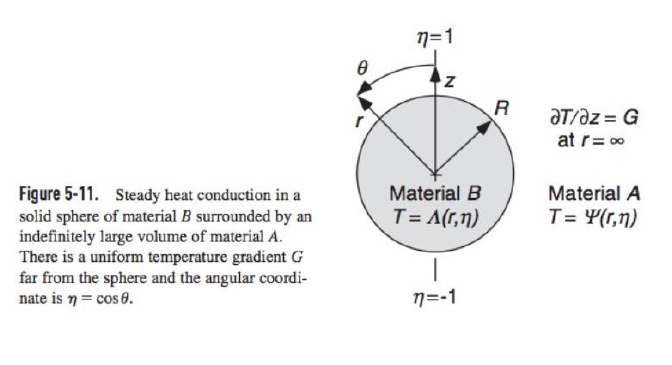
5-20. Concentrations of Reactive Solutes in Suspensions This problem concerns dilute suspensions of spheres in which a solute reacts irreversibly within the particles. It is desired to determine the steady concentration of the solute, inside and outside a sphere, created by an imposed concentration gradient in the bulk solution. As in Example 5.8-4, the spheres are of radius a, the sphere/liquid partition coefficient is K, and the imposed gradient at r= is C=Gez. There are no reactions in the liquid and the coordinates are as in Fig. 5-11. (a) Suppose that the reaction is zeroth order, with a volumetric rate of consumption k0. Show that the internal concentration (C) and external concentration (C) can each be constructed using linear superposition as C(r,)=C(r,)+h(r),C(r,)=C(r,)+H(r) where C and C are the corresponding solutions for an unreactive solute. Determine h(r) and H(r) and show that the concentration in the liquid is C(r,)=A+Gr+ra3(rG3Dk0) where is defined in Eq. (5.8-57). (Hint: The results in Example 5.8-4 make it unnecessary to repeat the solution for the unreactive case.) (b) Assume now that the reaction is first order, with a rate constant k1. Show that no solution exists for this case. EXAMPLE 5.8-4 Effective Diffusivity in a Suspension The effective diffusivity of a solute in a dilute suspension of spheres is derived now, following the approach originally employed by Maxwell (1873) for determining an effective electrical conductivity. Whereas the method used in Example 5.8-3 focuses on the gradient inside a sphere, the Maxwell approach is based on effects perceived far away. The continuous phase will be referred to as a liquid, although the results are equally applicable to other systems, such as solid spheres dispersed in another solid. The steady solute concentration in the liquid is expressed as C(r)=C(r)+C0(r) where C(r) is the concentration that would exist at position r if there were no particles present, and C0(r) is the perturbation caused by the particles. It is assumed that the unperturbed part of the concentration corresponds to a uniform imposed gradient, such that C is constant. For a dilute suspension, the contribution to C0 from each particle is that of an isolated sphere. In the absence of chemical reactions, the concentration field will be analogous to the temperature field determined in Example 5.8-2. Using the expression for the external temperature in Eq. (5.8-41), the concentration perturbation at r caused by a single sphere of radius a centered at r is c(r,r)=a3(2+1)(rr3rC),=DKDS The substitution Gr=Gz=rC was used. The solute diffusivities in the sphere and the surrounding fluid are denoted by DS and D, respectively, and K is the sphere-to-fluid concentration ratio at equilibrium. The reason that the partition coefficient appears in the diffusivity parameter is that the 5.8 FFT Solutions for Spherical Geometries 199 derivation of Eq. (5.841) assumed that the field variable was continuous at the phase boundary. Thus, with concentrations based on values in the liquid, the apparent diffusivity within the sphere is KDS. Suppose now that a suspension with n spheres per unit volume occupies a volume V, which is large enough to contain many particles and which is surrounded by pure liquid. For convenience, V itself is chosen to be a sphere (of radius R ). Summing the effects of all particles, the perturbation in the concentration far from V is C0(r)=nVc(r,r)dr The integration is over all particle positions r within V (the same as integrating over V ). The integral is simplified by recognizing that, at distant positions, the distinction between r and the origin (the center of V ) is insignificant. Approximating c(r,rr) by c(r,0), it is found that C0(r)=nVa3(2+1)(r3rC)=R3(2+1)(r3rC). The effective diffusivity in the suspension is calculated by comparing Eq. (5.8-55) with what is obtained by assuming that the volume V is occupied by a single phase. From Eq. (5.8-53), a homogeneous sphere of radius R, centered at the origin, will disturb the concentration in the surrounding fluid by the amount C0(r)=R3(2+1)(r3rC),=DKeffDeff where Keff and Deq are the effective partition coefficient and effective diffusivity, respectively. Equating C0 from Eqs. (5.8-55) and (5.8-56) gives (1)/(2+)=(1)/(2+), or =1+12,=2+1 Expanding the denominator for small and neglecting terms of O(2) leads to DKeffDeff=13(2+1)+O(2),=DKDS which is analogous to Eq. (5.8-51). A value of Deff/D cannot be obtained without knowing Keff. Specifying Keff is the same as defining the concentration that is to be used in conjunction with Deff. There are two common approaches. One is to base the suspension concentration on that in the liquid (continuous) phase. In that case, at equilibrium, the suspension concentration will equal that in the particle-free liquid surrounding V, and Keff=1. The other common approach is to use the volume-average concentration in the suspension, including both phases, which gives Keff=1+(K1). A frequent source of confusion in the literature is the failure to state which choice was made. This potential ambiguity does not arise in heat conduction because temperatures are continuous across phase boundaries. For the special case of impermeable spheres, setting =0 in Eq. (5.8-58) gives DDeff=123+O(2),DDeff=121+O(2),Keff=1Keff=1. The difference between these expressions underscores the need to define Keff. Equation (5.8-59) is analogous to the result obtained from Eq. (5.851) for perfectly insulating particles. Figure 5-11. Steady heat conduction in a solid sphere of material B surrounded by an indefinitely large volume of material A. There is a uniform temperature gradient G far from the sphere and the angular coordinate is =cos