

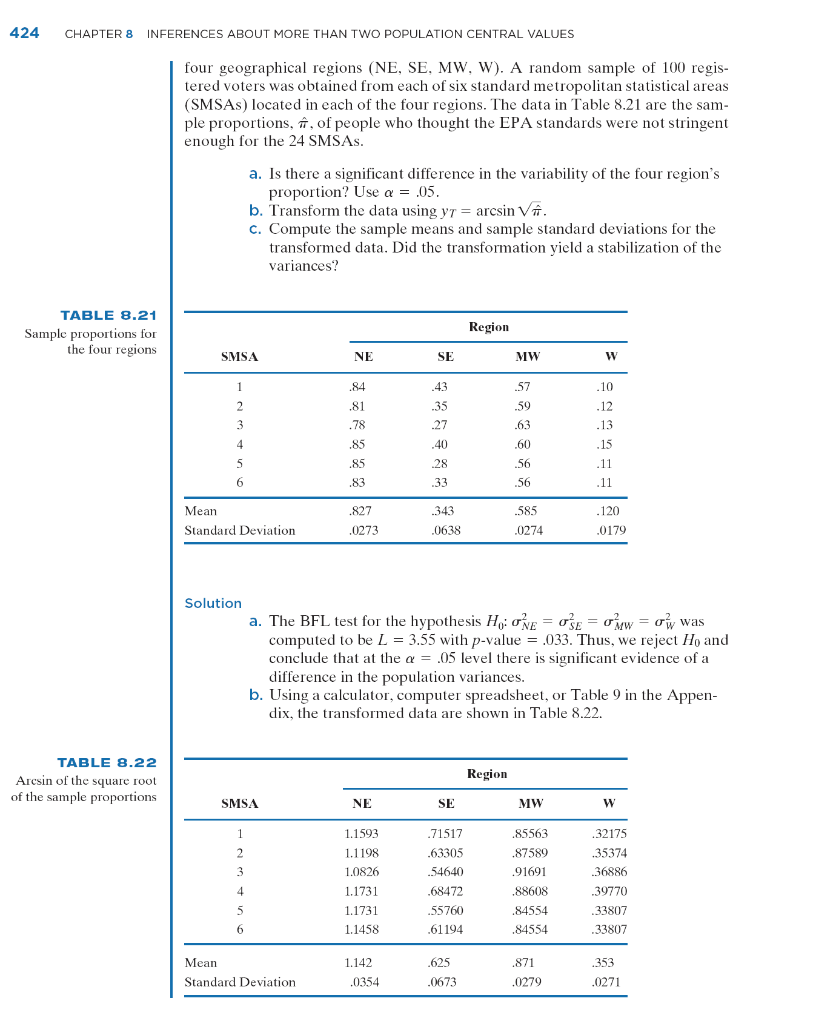

8.14 Refer to Example 8.6. a. Do the data indicate that the populations are not normally distributed? b. Do the transformed data appear to have a normal distribution? C. Does a transformation that produces data having equal variances guarantee that the transformed data will be normally distributed? A political action group conducted a national opinion poll to evaluate the voting public's opinion concerning whether the new EPA regulations on air pollution were stringent enough to protect the public's health. The group was also interested in determining if there were regional differences in the public's opinion concerning air pollution. For this poll, the country was divided into four geographical regions ( NE,SE,MW,W). A random sample of 100 registered voters was obtained from each of six standard metropolitan statistical areas (SMSAs) located in each of the four regions. The data in Table 8.21 are the sample proportions, ^, of people who thought the EPA standards were not stringent enough for the 24 SMSAs. a. Is there a significant difference in the variability of the four region's proportion? Use =.05. b. Transform the data using yT=arcsin^. c. Compute the sample means and sample standard deviations for the transformed data. Did the transformation yield a stabilization of the variances? TABLE 8.21 Sample proportions for the four regions Solution a. The BFL test for the hypothesis H0:NE2=SE2=MW2=W2 was computed to be L=3.55 with p-value =.033. Thus, we reject H0 and conclude that at the =.05 level there is significant evidence of a difference in the population variances. b. Using a calculator, computer spreadsheet, or Table 9 in the Appendix, the transformed data are shown in Table 8.22. TABLE 8.22 Arcsin of the square root of the sample proportions 8.6 A Nonparametric Alternative: The Kruskal-Wallis Test 425 c. We can observe that the standard deviations are more nearly alike than the standard deviations for the untransformed data. The BFL test for the hypothesis H0:NE2=SE2=MW2=W2 was computed for the transformed data. The results are given here. L=2.44 with p-value =.094. Thus, we fail to reject H0 and conclude that at the =.05 level there is not significant evidence of a difference in the variances of the transformed proportions. 8.14 Refer to Example 8.6. a. Do the data indicate that the populations are not normally distributed? b. Do the transformed data appear to have a normal distribution? C. Does a transformation that produces data having equal variances guarantee that the transformed data will be normally distributed? A political action group conducted a national opinion poll to evaluate the voting public's opinion concerning whether the new EPA regulations on air pollution were stringent enough to protect the public's health. The group was also interested in determining if there were regional differences in the public's opinion concerning air pollution. For this poll, the country was divided into four geographical regions ( NE,SE,MW,W). A random sample of 100 registered voters was obtained from each of six standard metropolitan statistical areas (SMSAs) located in each of the four regions. The data in Table 8.21 are the sample proportions, ^, of people who thought the EPA standards were not stringent enough for the 24 SMSAs. a. Is there a significant difference in the variability of the four region's proportion? Use =.05. b. Transform the data using yT=arcsin^. c. Compute the sample means and sample standard deviations for the transformed data. Did the transformation yield a stabilization of the variances? TABLE 8.21 Sample proportions for the four regions Solution a. The BFL test for the hypothesis H0:NE2=SE2=MW2=W2 was computed to be L=3.55 with p-value =.033. Thus, we reject H0 and conclude that at the =.05 level there is significant evidence of a difference in the population variances. b. Using a calculator, computer spreadsheet, or Table 9 in the Appendix, the transformed data are shown in Table 8.22. TABLE 8.22 Arcsin of the square root of the sample proportions 8.6 A Nonparametric Alternative: The Kruskal-Wallis Test 425 c. We can observe that the standard deviations are more nearly alike than the standard deviations for the untransformed data. The BFL test for the hypothesis H0:NE2=SE2=MW2=W2 was computed for the transformed data. The results are given here. L=2.44 with p-value =.094. Thus, we fail to reject H0 and conclude that at the =.05 level there is not significant evidence of a difference in the variances of the transformed proportions










