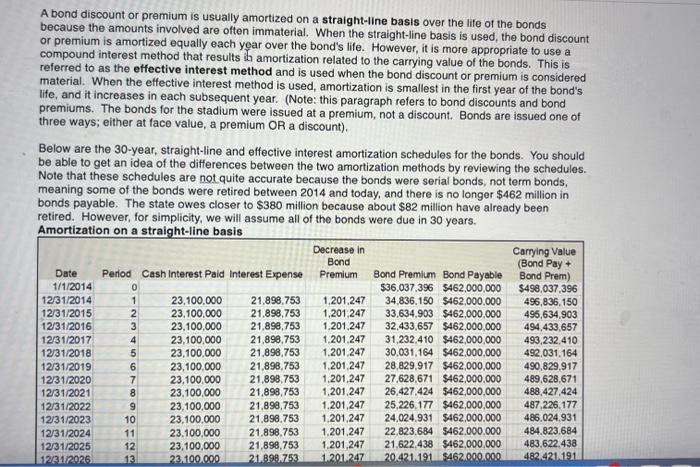
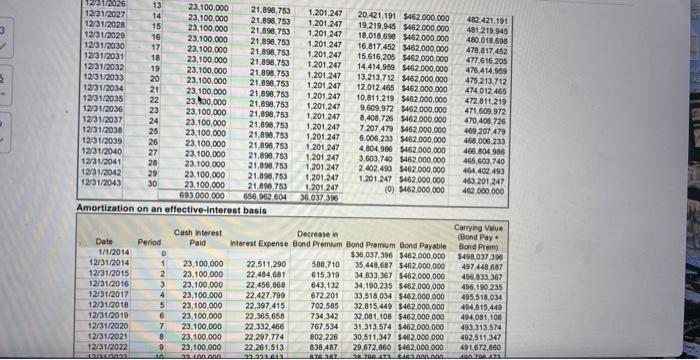
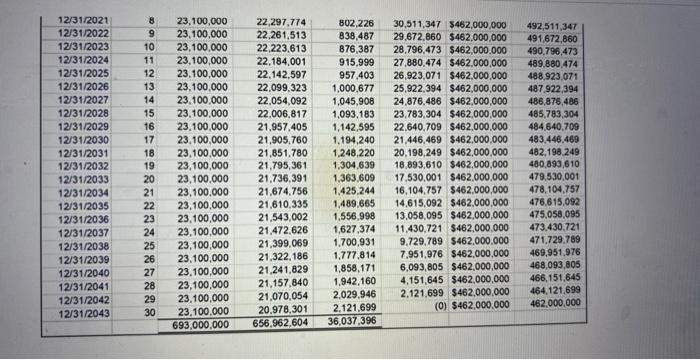
A bond discount or premium is usually amortized on a straight-line basis over the life of the bonds because the amounts involved are often immaterial. When the straight-line basis is used, the bond discount or premium is amortized equally each year over the bond's life. However, it is more appropriate to use a compound interest method that results in amortization related to the carrying value of the bonds. This is referred to as the effective interest method and is used when the bond discount or premium is considered material. When the effective interest method is used, amortization is smallest in the first year of the bond's life, and it increases in each subsequent year. (Note: this paragraph refers to bond discounts and bond premiums. The bonds for the stadium were issued at a premium, not a discount. Bonds are issued one of three ways; either at face value, a premium OR a discount). Below are the 30-year, straight-line and effective interest amortization schedules for the bonds. You should be able to get an idea of the differences between the two amortization methods by reviewing the schedules. Note that these schedules are not quite accurate because the bonds were serial bonds, not term bonds, meaning some of the bonds were retired between 2014 and today, and there is no longer $462 million in bonds payable. The state owes closer to $380 million because about $82 million have already been retired. However, for simplicity, we will assume all of the bonds were due in 30 years. Amortization on a straight-line basis Date Period Cash Interest Paid Interest Expense 1/1/2014 12/31/2014 12/31/2015 12/31/2016 12/31/2017 12/31/2018 12/31/2019 12/31/2020 12/31/2021 12/31/2022 12/31/2023 12/31/2024 12/31/2025 12/31/2026 0 1 2 3 4 5 6 7 8 9 10 11 12 13 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23.100.000 Decrease in Bond Premium 21,898,753 1,201,247 21,898,753 1,201,247 21,898,753 1,201,247 21,898,753 21,898,753 21,898,753 21,898,753 21,898,753 21,898,753 21,898,753 21,898,753 21.898.753 1,201,247 31,232,410 $462,000,000 30,031,164 $462,000,000 1,201,247 1,201,247 Bond Premium Bond Payable $36,037,396 $462,000,000 34,836,150 $462,000,000 33,634,903 $462,000,000 32,433,657 $462,000,000 28,829,917 $462,000,000 1,201,247 27,628,671 $462,000,000 1,201,247 26,427,424 $462,000,000 1,201,247 1,201,247 21,898,753 1,201,247 25,226.177 $462,000,000 24,024.931 $462,000.000 22,823,684 $462,000,000 1,201,247 21,622,438 $462,000,000 1.201.247 20.421.191 $462.000.000 Carrying Value (Bond Pay + Bond Prem) $498,037,396 496,836,150 495,634,903 494,433,657 493,232,410 492,031,164 490,829,917 489,628,671 488,427,424 487,226,177 486.024.931 484.823.684 483,622,438 482.421.191 3 S 12/31/2026 12/31/2027 12/31/2028 12/31/2029 12/31/2030 12/31/2031 12/31/2032 12/31/2033 12/31/2034 12/31/2035 12/31/2036 12/31/2037 12/31/2038 12/31/2039 12/31/2040 12/31/2041 12/31/2042 12/31/2043 212212222232222222 14 15 16 17 18 19 20 24 25 26 27 28 29 30 Date Period 1/1/2014 12/31/2014 12/31/2015 12/31/2016 12/31/2017 12/31/2018 12/31/2019 12/31/2020 12/31/2021 12/31/2022 1010023 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,00,000 10 23,100,000 21.898,753 21,898,753 21,898,753 1,201,247 1,201,247 1,201,247 1,201,247 1,201,247 1,201,247 1,201,247 1,201,247 23,100,000 21,898,753 1,201,247 23,100,000 21,890.753 1,201,247 23,100,000 21,898,753 1,201,247 23,100,000 21,898,753 1.201.247 23,100,000 21,898,753 1,201.247 23,100,000 21.890,753 1,201,247 21.890,753 1,201,247 656,962.604 36.037.396 23,100,000 693,000,000 Amortization on an effective-interest basis Cash Interest Paid 0 1 23,100,000 2 23,100,000 3 23,100,000 4 23,100,000 5 23,100,000 6 23,100,000 7 23,100,000 8 23,100,000 23,100,000 22.100.000. 21,898,753 21,898,753 21.898,753 21,898,753 21,898,753 21,898,753 21,898,753 21,898,753 1,201,247 1,201,247 1,201,247 22,511,290 22,484,681 22.456,868 22,427,799 22,397,415 22,365,658 22.332,466 22,297,774 22,261,513 22.221.611. 20.421,191 $462.000.000 19.219.945 $462.000.000 18,018.690 $462.000.000 16,817.452 $462,000,000 15.616,205 $462,000,000 14,414,959 $462.000.000 13.213.712 $462,000,000 12.012.465 $462.000.000 10,811,219 $462.000.000 9.609.972 $462,000,000 8.408.726 $462.000.000 7.207.479 $462.000.000 6.006,233 $462.000,000 4,804.986 $462,000,000 3,603.740 $462.000.000 2.402.493 $462.000.000 1.201.247 $462.000.000 (0) $462,000,000 Decrease in t Interest Expense Bond Premium Bond Premium Bond Payable $36,037.396 $462,000,000 580,710 35,448,687 $462,000,000 615,319 34,833.367 $462,000,000 643,132 34,190,235 $462,000,000 672.201 33,518,034 $462.000.000 702,585 32,815,449 $462,000,000 734,342 32,081,108 $462,000,000 767,534 31,313,574 $462,000,000 802,226 30,511,347 $462,000,000 838,487 29,672,860 $462,000,000 32.706 473 $462.000.000 878 187 482,421.191 481,219,945 480,018,698 478.817.452 477,616.205 476,414,959 475.213.712 474,012.465 472.811,219 471,609,972 470.408.726 469,207,479 468.006.233 466,804.906 465,603,740 464,402.493 463.201.247 462,000,000 Carrying Value (Bond Pay Bond Prem) $498,037,396 497,448,687 496,833.367 496,190,235 495,518,034 494,815,449 494,081, 108 493,313.574 492,511,347 491,672.860 400.700 423 12/31/2021 12/31/2022 12/31/2023 12/31/2024 12/31/2025 12/31/2026 12/31/2027 12/31/2028 12/31/2029 12/31/2030 12/31/2031 12/31/2032 12/31/2033 12/31/2034 12/31/2035 12/31/2036 12/31/2037 12/31/2038 12/31/2039 12/31/2040 12/31/2041 12/31/2042 12/31/2043 23,100,000 9 23,100,000 10 23,100,000 11 23,100,000 12 23,100,000 13 23,100,000 14 23,100,000 15 23,100,000 16 23,100,000 17 23,100,000 18 23,100,000 19 23,100,000 20 23,100,000 23,100,000 23,100,000 23 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 23,100,000 2,029,946 23,100,000 20,978,301 2,121,699 693,000,000 656,962.604 36,037,396 21 22 24 25 26 27 28 29 22,297,774 22,261,513 22,223,613 22,184,001 915,999 22,142,597 957,403 22,099,323 1,000,677 22,054,092 1,045,908 22,006,817 1,093,183 21,957,405 21,905,760 1,194,240 21,851,780 1,248,220 21,795,361 1,304,639 21,736.391 1,363,609 21,674,756 1,425,244 21,610,335 1,489,665 21,543,002 1,556,998 21,472,626 1,627,374 21,399,069 1,700,931 21,322,186 1,777,814 21,241,829 1,858,171 21,157,840 1,942,160 21,070,054 30 802,226 30,511,347 $462,000,000 492,511,347 838,487 29,672,860 $462,000,000 491,672,860 876,387 28,796,473 $462,000,000 27,880,474 $462,000,000 26,923,071 $462,000,000 25,922,394 $462,000,000 24,876,486 $462,000,000 23,783,304 $462,000,000 1,142,595 22,640,709 $462,000,000 21,446,469 $462,000,000 20,198,249 $462,000,000 18,893,610 $462,000,000 17,530,001 $462,000,000 16,104,757 $462,000,000 14,615,092 $462,000,000 13,058,095 $462,000,000 11,430,721 $462,000,000 9,729,789 $462,000,000 7.951,976 $462,000,000 6,093,805 $462,000,000 4,151,645 $462,000,000 2,121,699 $462,000,000 (0) $462,000,000 490,796,473 489,880,474 488,923.071 487,922,394 486,876,486 485,783,304 484,640,709 483,446,469 482,198,249 480,893,610 479,530,001 478,104,757 476,615,092 475,058,095 473,430,721 471,729,789 469,951,976 468,093,805 466,151,645 464,121,699 462,000,000 Explain how is the cash interest paid of $23,100,000 calculated? Note that this amount stays the same for the entire 30 years under both amortization methods. Explain why is interest expense recorded by the state and city each period less than the $23,100,000 of cash interest paid? (Note: This is true for both amortization methods.) (Hint: the bonds were issued at a premium). Look at the effective interest amortization schedule. In the first year, interest expense of $22,511,290 is recorded. To get this amount, we multiply the market interest rate times the bond carrying value to calculate interest expense. Therefore, what is the bond's market interest rate? a) 4.87% b) 4.52% O c) 5.0%