Answered step by step
Verified Expert Solution
Question
1 Approved Answer
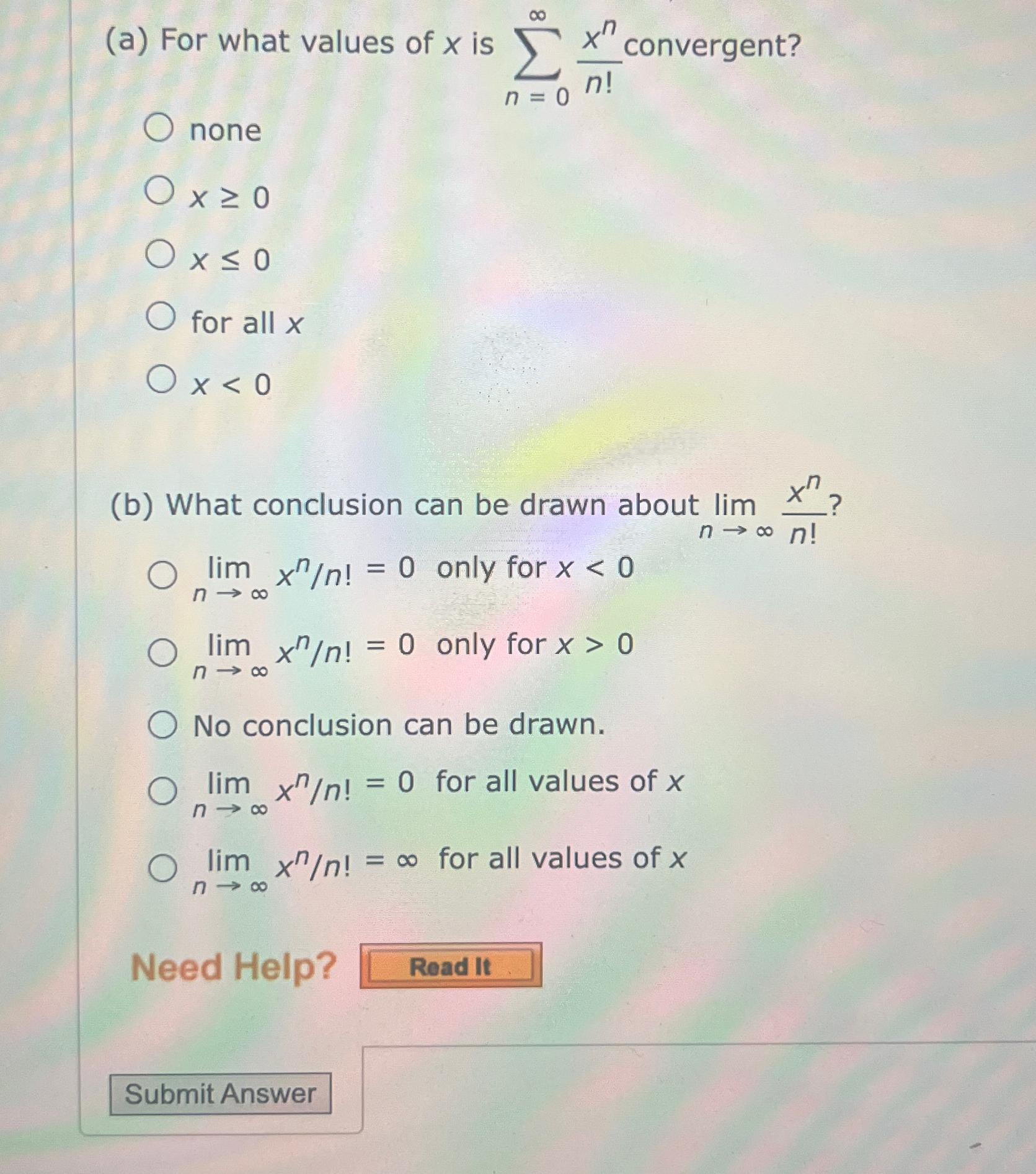
(a) For what values of x is sum_(n=0)^(infty ) (x^(n))/(n!) convergent? none x>=0 x for all x x (b) What conclusion
(a) For what values of
xis
\\\\sum_(n=0)^(\\\\infty ) (x^(n))/(n!)convergent? none\
x>=0\
x\ for all
x\
x\ (b) What conclusion can be drawn about
\\\\lim_(n->\\\\infty )(x^(n))/(n!) ?\
\\\\lim_(n->\\\\infty )(x^(n))/(n)!=0 only for
x\
\\\\lim_(n->\\\\infty )(x^(n))/(n)!=0 only for
x>0\ No conclusion can be drawn.\
\\\\lim_(n->\\\\infty )(x^(n))/(n)!=0 for all values of
x\
\\\\lim_(n->\\\\infty )(x^(n))/(n)!=\\\\infty for all values of
x\ Need Help?
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


