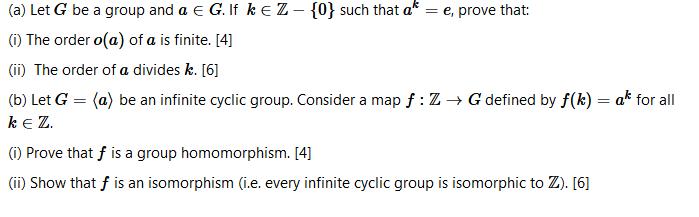Question
(a) Let G be a group and a E G. If kEZ- {0} such that af = e, prove that: (1) The order o(a)
(a) Let G be a group and a E G. If kEZ- {0} such that af = e, prove that: (1) The order o(a) of a is finite. [4] (ii) The order of a divides k. [6] (b) Let G = (a) be an infinite cyclic group. Consider a map f : Z G defined by f(k) = ak for all ke Z. (i) Prove that f is a group homomorphism. [4] (ii) Show that f is an isomorphism (i.e. every infinite cyclic group is isomorphic to Z). [6]
Step by Step Solution
3.43 Rating (156 Votes )
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get StartedRecommended Textbook for
Discrete and Combinatorial Mathematics An Applied Introduction
Authors: Ralph P. Grimaldi
5th edition
201726343, 978-0201726343
Students also viewed these Mathematics questions
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
View Answer in SolutionInn App