A physicist has proposed a theory according to which in a Bell-experiment involving a pair of photons, each pair of photons is marked by a polarization that is unknown, yet defined beforehand, and identical to both photons. In order to verify his postulates, he carries out two experiments in order to check the correlation in polarization between the pairs of photons.

Experiment A:

A Bell-type of experiment with pairs of entangled photons of identical polarization.

Experiment B:

Each pair 'i' of photons first passes through a pair of polarisers with identical polarisation at angle _i (the results at the detectors are taken into consideration only in case both photons passed the first pair of polarisers, that is to say, they create a given identical polarisation in both photons). The angle _i is set each time by a computer and changes randomly from pair to pair (with a uniform distribution across all different directions of the polarisers).

In each one of the experiments, polariser A is kept at a constant angle of =0 degrees, while the angle of polariser B is gradually altered within the range of 0

The correlation for the different angles are measured.

The rate of mismatches between the results measured by the polarisers is denoted by E().

a) write out the formula and draw a graph for E() in Experiment A.

b) for experiment A, using one single system of axes, draw the graphs of functions 2E(), E(2), within the range of 0

c) answer without calculations:

do you expect the Bell inequalities to always hold in Experiment B, or will they be violated? Explain your answer.

d) calculate the probability that a photon with given angle _i will pass polariser A and that its partner will not pass polariser B (express the probability by using _i and _B).

e) as mentioned before, across many experiments, _i changes randomly. Calculate the average of the probabilities that you calculated in the previous paragraph within the range of 0

f) using one single system of axes of functions, draw the graphs of functions 2E(), E(2), within the range of 0

Tools:

1)

remember, the average of function f(x) within range [a,b] is:

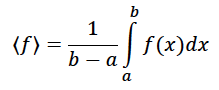
2)

you can use the following integral:

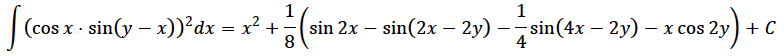
THANK YOU VERY MUCH!

S co KE A B A B b (f) -a f(x)dx b - a 1 |(cos x = sin(y x)?dx = x + als ( sin 2x sin(2x 2y) --sin(4x 2y) x cos 2y) + C 4 S co KE A B A B b (f) -a f(x)dx b - a 1 |(cos x = sin(y x)?dx = x + als ( sin 2x sin(2x 2y) --sin(4x 2y) x cos 2y) + C 4