(a) Prove, by induction on the number of nodes, n that an s-tree always has a number of black nodes that is 1 more than the number of green nodes. Dont forget to include the BC, IH, and IS.

b) Prove, by induction on the height, h that any s-tree has an odd number of nodes (recall that a number is odd if it can be written as 2x + 1 for some integer x). Dont forget to include the BC, IH, and IS.

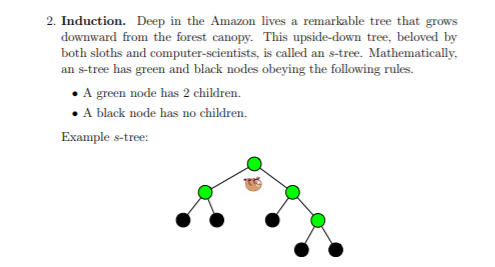
2. Induction. Deep in the Amazon lives a remarkable tree that grows downward from the forest canopy. This upside down tree, beloved by both sloths and computer-scientists, is called an s-tree. Mathematically, an s-tree has green and black nodes obeying the following rules. A green node has 2 children. A black node has no children. Example s-tree