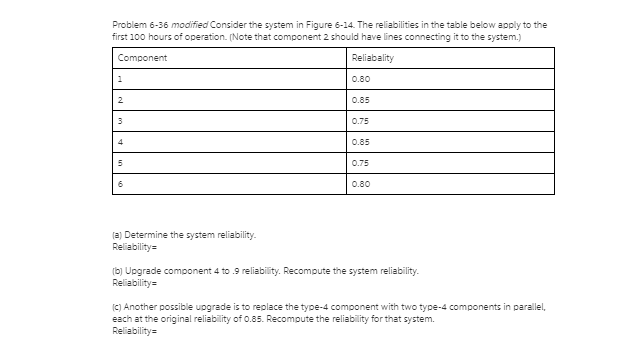
(a) Prove that the centrifugal stress at the root of an untapered blade attached to the drum of an

axial flow turbomachine is given by

?c ??mN2

Ax=1800,

where ?m density of blade material, N rotational speed of drum, in rpm and Ax area of

the flow annulus.

(b) The preliminary design of an axial-flow gas turbine stage with stagnation conditions at stage

entry of p01 400 kPa, T01 850 K, is to be based upon the following data applicable to the

mean radius:

Flow angle at nozzle exit, ?2 63.8;

Reaction, R 0.5;

Flow coefficient, cx/Um 0.6;

Static pressure at stage exit, p3 200 kPa;

Estimated total-to-static efficiency, ?ts 0.85.

Assuming that the axial velocity is unchanged across the stage, determine

(i) the specific work done by the gas;

(ii) the blade speed;

(iii) the static temperature at stage exit.

(c) The blade material has a density of 7850 kg/m3 and the maximum allowable stress in the

rotor blade is 120 MPa. Taking into account only the centrifugal stress, assuming untapered

blades and constant axial velocity at all radii, determine for a mean flow rate of 15 kg/s

(i) the rotor speed (rev/min);

(ii) the mean diameter;

(iii) the hub-tip radius ratio.

For the gas assume that CP 1050 J/(kg K) and R 287 J/(kg K).

11. The design of a single-stage axial-flow turbine is to be based on constant axial velocity with axial

discharge from the rotor blades directly to the atmosphere. The following design values have

been specified:

Mass flow rate 16.0 kg/s

Initial stagnation temperature, T01 1100

11. Suppose we have 8 teams labeled T1, . . . , T8. Suppose they are ordered by placing

their names in a hat and drawing the names out one at a time.

(a) How many ways can it happen that all the odd numbered teams are in the odd

numbered slots and all the even numbered teams are in the even numbered slots?

(b) What is the probability of this happening?

12. (Taken from the book by Dekking et. al. problem 4.9) The space shuttle has 6 O-rings

(these were involved in the Challenger disaster). When launched at 81? F, each O-ring has

a probability of failure of 0.0137 (independent of whether other O-rings fail).

(a) What is the probability that during 23 launches no O-ring will fail, but that at least

one O-ring will fail during the 24th launch of a space shuttle?

(b) What is the probability that no O-ring fails during 24 launches

1. Each year, ratings are compiled concerning the performance of new cars during the first 90 days of use. Suppose that the cars have been categorized according to whether the car needs warranty-related repair (yes or no) and the country in which the company manufacturing the car is based (U.S. or not U.S.). Based on the data collected, the probability that the new car needs a warranty repair is 0.04, the probability that the new car is manufactured by a U.S. based company is 0.60, and the probability that the new car needs a warranty repair and was manufactured by a U.S. based company is 0.025. a. Construct a contingency table to evaluate the probabilities. b. Give an example of a simple event. c. Give an example of a joint probability. d. What is the complement of "a car is manufactured by a company based in the United States"? e. What is the probability that a randomly chosen car needs a warranty repair? f. What is the probability that a randomly chosen car was not manufactured by a company based in the United States? g. What is the probability that a randomly chosen car does not need a warranty repair? h. What is the probability that a randomly chosen car was manufactured by a company based in the United States? i. What is the probability that a randomly chosen car was manufactured by a company based in the United States and does not need a warranty repair? i. What is the probability that a randomly chosen car needs a warranty repair and was not manufactured by a company based in the United States? k. What is the probability that a randomly chosen car was manufactured by a company based in the United States and needs a warranty repair? I. What is the probability that a randomly chosen car needs a warranty repair or was manufactured by a company based in the United States? m. What is the probability that a randomly chosen car was not manufactured by a company based in the United States or does not need a warranty repair? n. Suppose we choose a car that does not need a warranty repair, then what is the probability that it was not manufactured by a company based in the United States? o. Does the country of manufacture influence whether the car needs to be repaired or not?\f3. Assuming degrees of freedom = 22, and you are interested in obtaining a confidence interval for the middle 90% of values, what would your / value be? 4. According to national employment statistics, employees at Company Y, a local manufacturing company, earned a starting salary of u= $50,000 with o= $10,440. Assume you take a sample of 36 new employees. What is the probability the average salary of this sample will be between $48,000 and $52,000?Statistics Quiz 2 Name: Date: A country conducts a study of new cars within the first 90 days of use. The cars have been categorized according to whether the car needs a warranty-based repair (yes or no) and the car's origin (domestic or foreign). Based on the data collected, the probability that the new car needs warranty repair is 0.09, the probability that the car was manufactured by a domestic company is 0.73, and the probability that the new car needs a warranty repair and was manufactured by a domestic company is 0.029. Complete the contingency table found below to evaluate the probabilities of a warranty-related repair. Yes (Y) No (Y') Domestic(D) Foreign (D') 1. What is the probability that a new car selected at random needs a warranty repair? 2. What is the probability that a new car selected at random does not need a warranty repair? 3. What is the probability that a new car selected at random is foreign manufactured? 4. What is the probability that a new car selected at random is domestically manufactured? 5. What is the probability that a new car selected at random needs a warranty repair and is domestically manufactured? 6. What is the probability that a new car selected at random needs a warranty repair or was manufactured by a domestic company