Question
A rational number is a number that can be expressed as a fraction of the form a/b, where a is the numerator and b is
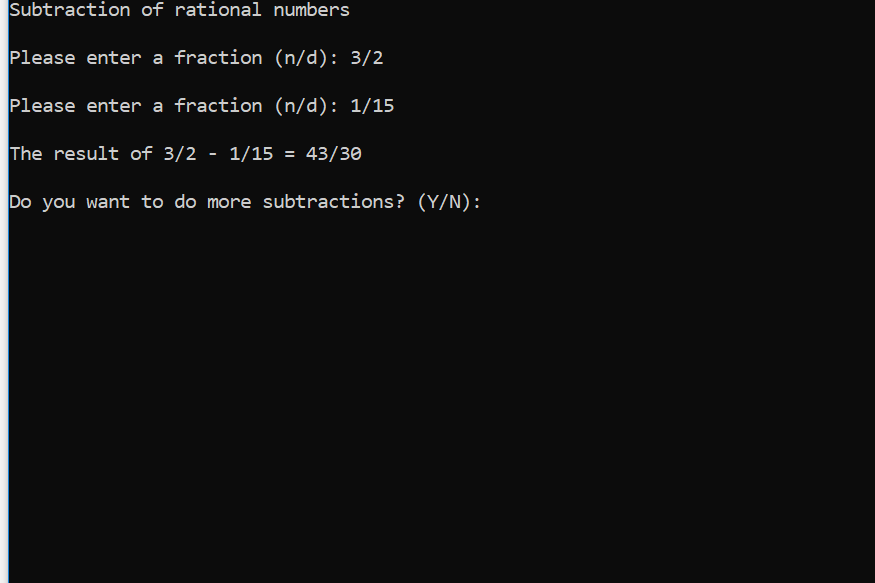
A rational number is a number that can be expressed as a fraction of the form a/b, where a is the numerator and b is the denominator and both are integers. Arithmetic operations on two rational numbers a/b and c/d are defined as follows: Addition: a + c = (a * d) + (c * b) b d (b * d) Subtraction: a - c = (a * d) - (c * b) b d (b * d) Write an interactive program that presents the following menu to the user: _______________________________________________________________________________ Rational numbers calculator (A)ddition (S)ubtraction (Q)uit Enter your option:_ _______________________________________________________________________________ The menu must be displayed by a void function named showMenu(). This function just shows the title and the options, the decision whether to call add(), subtract(), or quit must be done in main(). The Addition and Subtraction options must be implemented by a couple of void functions named add() and subtract()respectively. These functions must clear the screen and show a title specifying the operation to be performed. Next, they have to show a couple of input prompts asking for the rational numbers and, after getting and processing them, they have to display the result. After performing their corresponding operations, the functions must ask the user whether he/she would like to do more operations. If the user chooses to do more operations, the functions repeat the steps described in the previous paragraph (that is, they clear the screen, ask for both numbers, and so forth). This process is repeated for as long as the user chooses to. When the user is done with an operation, the menu must be shown again. All the letters entered by the user as an answer to a question posted by the program must be accepted in upper or lower case. The screen shown by these functions should look like this: Addition of rational numbers Please enter a fraction (n/d): 1/2 (entered by the user) Please enter a fraction (n/d): 2/4 (entered by the user) The result of 1/2 + 2/4 = 1 Do you want to do more additions? (Y/N): The different operations on the rational numbers must be implemented using the following functions: GetRational(int num, int den); // This function shows the prompt Please enter a fraction (n/d): , gets the values // from the keyboard and returns them to the caller. Since the division operator (/) // is read in along with the numbers the function must read and discard it. // This function must reject a denominator equal to zero. AddRational(int anum, int aden, int num1, int den1, int num2, int den2); // num1, den1, num2, and den2 are provided by the caller. // anum and aden are calculated using the formula shown above and returned to the // caller after they are reduced. To reduce the fraction this function must call // the function reduce(anum, aden). SubtractRational(int anum, int aden, int num1, int den1, int num2, int den2); // num1, den1, num2, and den2 are provided by the caller. // anum and aden are calculated using the formula shown above and returned to the // caller after they are reduced. To reduce the fraction this function must call // the function reduce(anum, aden). DisplayRational(int num, int den); // num and den are provided by the caller. // The numbers are shown in the form num/den unless den is equal to 1, in this case // only the numerator should be displayed. reduce(int num, int den) // num and den are provided by the caller. // num and den are reduced according to the algorithm explained below and returned to // the caller. These functions must be called by add() and subtract() to perform the corresponding operations. Note: all the functions must be defined in a header file named hw4functions.h IMPORTANT: ? You must define whether each function is a void or a value-returning function. ? You must define whether each parameter is a value parameter or a reference parameter. ? You must use the identifiers I provide you for the parameters and functions. ? You must use the following algorithm to reduce the fraction. To reduce a fraction, you need to find the greatest common factor (gcf) of the numerator and denominator. Once it is found, divide both the numerator and denominator by the absolute value of the gcf. The greatest common factor of two integers is the largest integer that will divide both numbers evenly. For example, the greatest common factor of 18 and 27 is 9, since 9 is the largest integer to divide evenly into both 18 and 27. Since 9 goes into 18 twice and into 27 three times, the reduced fraction is 2/3. An efficient algorithm for computing the gcf is attributed to the Greek mathematician Euclid (ca. 300 B.C.). Euclid's algorithm: 1. let A and B be two positive integers 2. let R = remainder after dividing A by B 3. while R != 0 A = B B = R R = remainder after dividing A by B 4. B is the gcf Example: suppose you need to reduce the fraction 24/60 First you find the gcf of 24 and 60: A = 24, B = 60 24/60 is 0 with remainder R = 24 set A = 60, B = 24 60/24 is 2 with remainder R = 12 set A = 24, B = 12 24/12 is 2 with remainder R = 0 So, the gcf is 12. Then, you need to divide 24 by 12 and 60 by 12 to get the fraction reduced. The resulting fraction is 2/5. For your reference, I am providing you the executable of my solution. Test both programs (yours and mine) with the different sets of input values shown below and compare their results to ensure that your program is showing exactly the same results that mine is showing (pay attention to the output generated by both programs). Test plans: Set of inputs to be used to test the program: A) 1/2 and 2/4 B) 1/3 and 3/4 C) 9/5 and 3/0 (this entry should be rejected so reenter 2/5) Use them to test both operations (add and subtract). To clear the screen, use system("cls") (Windows) or system("clear") (Mac) Since system("pause") works only on Windows, use the lines of code shown below to pause your program (Windows and Mac): // This is to pause the execution of the program cout 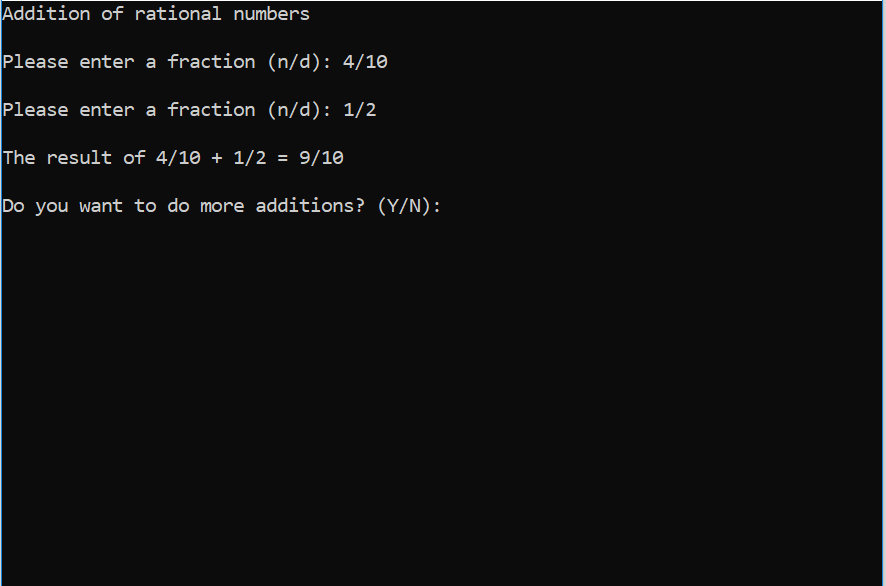
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


