Question: A Small Numerical Library Here is header : #ifndef __MATHLIB_H__ #define __MATHLIB_H__ double Sin(double x); double Cos(double x); double Tan(double x); double Exp(double x); double










A Small Numerical Library
Here is header :
#ifndef __MATHLIB_H__ #define __MATHLIB_H__ double Sin(double x); double Cos(double x); double Tan(double x); double Exp(double x); double Log(double x); #endif
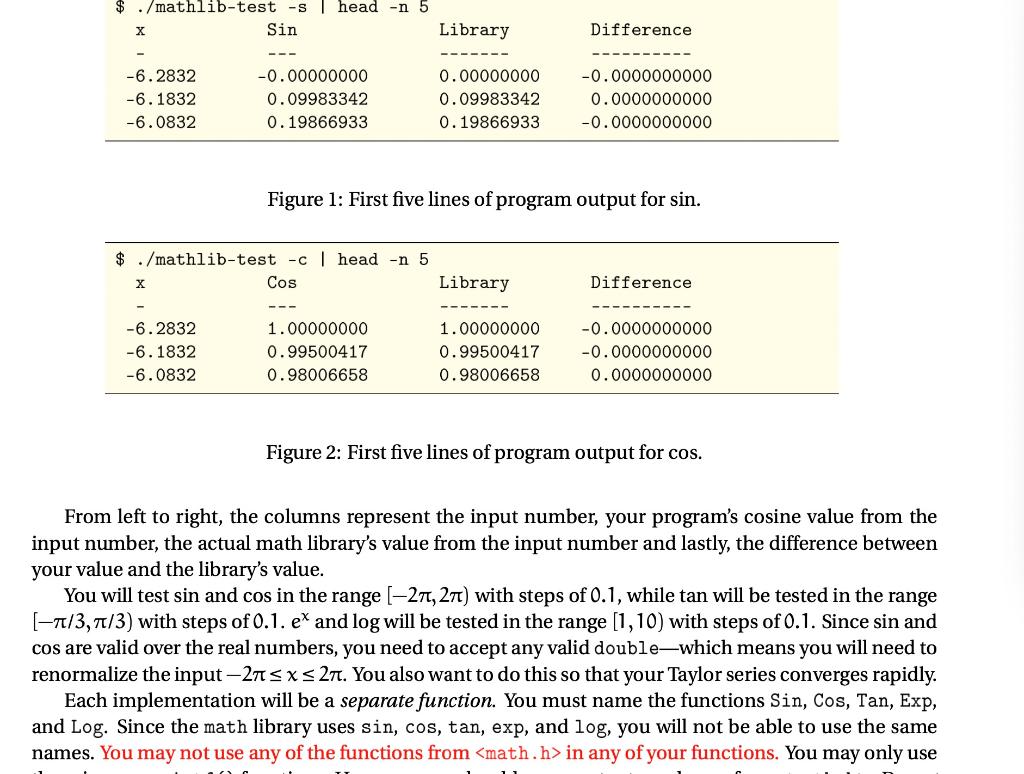
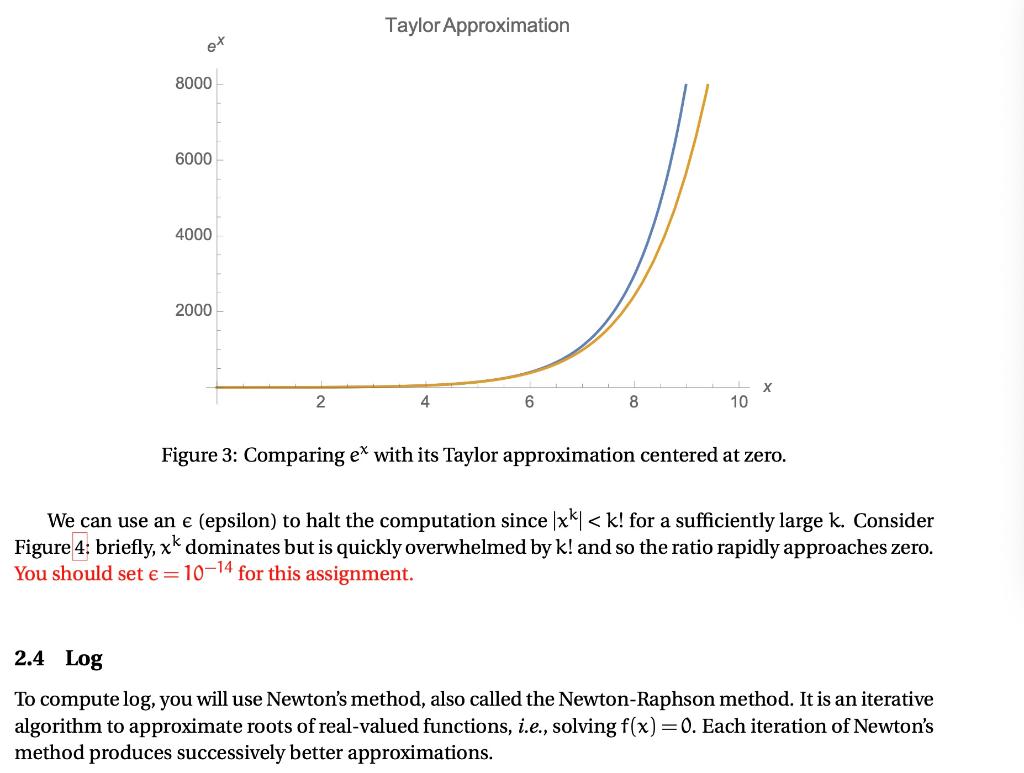
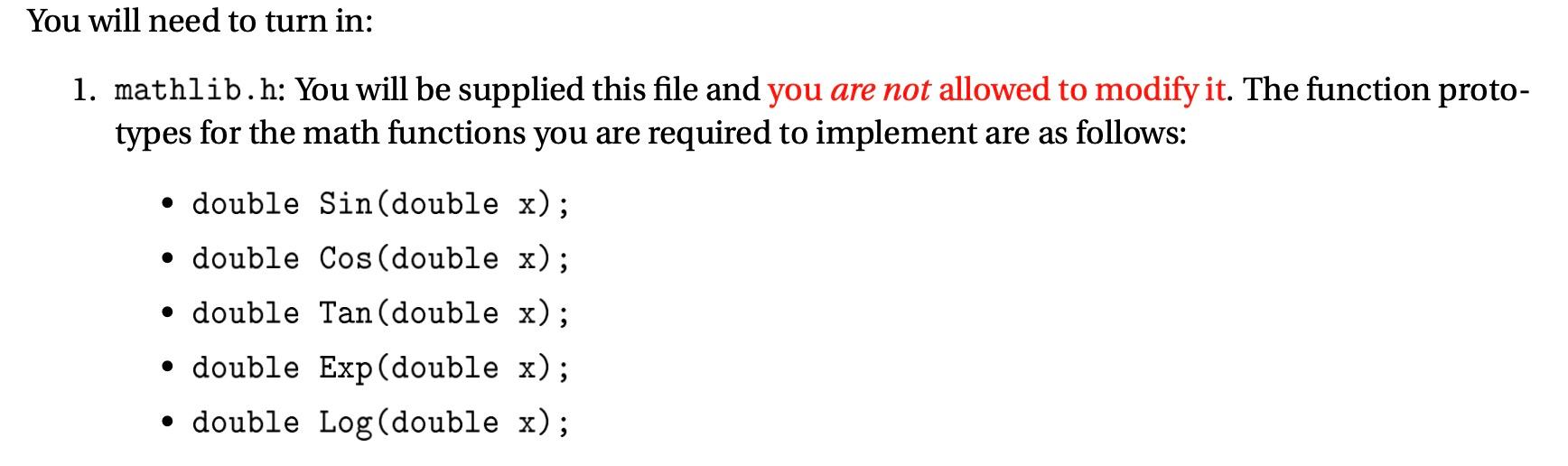
As we know, computers are simple machines that carry out a sequence of very simple steps, albeit very quickly. Unless you have a special-purpose processor, a computer can only compute addition, subtrac- tion, multiplication, and division. If you think about it, you will see that the functions that might interest you when dealing with real or complex numbers can be built up from those four operations. We use many of these functions in nearly every program that we write, so we ought to understand how they are created. If you recall from your calculus class, with some conditions a function f(x) can be represented by its Taylor series expansion near some point f(a): f(k) (a) f(x) =f(a)+ (x-a). k! k=1 Note: when you see I, you should generally think of a for loop. If you have forgotten (or never taken) calculus, do not despair. Go to a laboratory section for review: the concepts required for this assignment are just derivatives. Since we cannot compute an infinite series, we must be content to calculate a finite number of terms. In general, the more terms that we compute, the more accurate our approximation. For example, if we expand to 10 terms we get: f(3)(a) f(1)(a) f(2)(a) f(4)(a) f(x)=f(a) + (x-a)' + -(x-a)?+ (x-a)3 + (x-a)* 1! 2! 3! 4! f(5)(a) f(6)(a) +(x-a)5 + f17)(a) f(8)(a) a) + (x- (x-a) + (x- -a) 5! 6! 7! 8! f(!)(a) (x - a)?+Of(x-a)''). 9! + + Note: k!=k(k-1)(k-2)... x1, and by definition, O!=1. Taylor series, named after Brook Taylor, requires that we pick a point a where we will center the approximation. In the case a =0, then it is called a Maclaurin series). Often we choose 0, but the closer to the value of x the better we will approximate the function. For example, let's consider ex centered around 0: X5 x6 xk k! = 1+ x x2 + 1! 2! + x3 x4 + 3! 4! + x7 x8 x + + +... + 5! 6! 7! 8! 9! k=0 This is one of the simplest series when centered at 0, since e=1. Consider the general case: ea ea ea ea ere + (x-a (x- ea + a) (x a)" + (x 2! -a)' + 3! 1! 4! ea ea ea a)4+ (x- 5! a) + (x 10! ea ea + + (x 6! a (x-a)' + (x-a) + (x- 10 -a) +0(x-a)"). 8! 9! Since dex = ex the exponential function does not drop out as it does for a=0, leaving us with our original problem. If we knew e for a = x then we could use a small number of terms. However, we do not know it and so we must use a=0. What is the O((x - a)") term? That is the error term that is on the order of the value in parentheses. This is different from the big-O that we will discuss with regard to algorithm analysis. For this assignment, you will be creating a small numerical library and a corresponding test harness. Our goal is for you to have some idea of what must be done to implement functions that you use all the time. You will be writing and implementing sin, cos, tan, ex, and log. You will use Taylor series approxima- tion for sin, cos, tan, and ex, and use Newton's method to approximate log. You will then compare your implemented functions to the corresponding implementations in the standard library with a test harness and output the results into a table similar to what is show in Figures 1 and 2. $ ./mathlib-test -s head -n 5 X Sin Library Difference -6.2832 -6.1832 -6.0832 -0.00000000 0.09983342 0.19866933 0.00000000 0.09983342 0.19866933 -0.0000000000 0.0000000000 -0.0000000000 Figure 1: First five lines of program output for sin. $ ./mathlib-test - head -n 5 Cos X Library Difference -6.2832 -6.1832 -6.0832 1.00000000 0.99500417 0.98006658 1.00000000 0.99500417 0.98006658 -0.0000000000 -0.0000000000 0.0000000000 Figure 2: First five lines of program output for cos. From left to right, the columns represent the input number, your program's cosine value from the input number, the actual math library's value from the input number and lastly, the difference between your value and the library's value. You will test sin and cos in the range [-271, 27t) with steps of 0.1, while tan will be tested in the range [-1/3,1/3) with steps of 0.1. ex and log will be tested in the range [1,10) with steps of 0.1. Since sin and cos are valid over the real numbers, you need to accept any valid double-which means you will need to renormalize the input-271s x s 27. You also want to do this so that your Taylor series converges rapidly. Each implementation will be a separate function. You must name the functions Sin, Cos, Tan, Exp, and Log. Since the math library uses sin, cos, tan, exp, and log, you will not be able to use the same names. You may not use any of the functions from in any of your functions. You may only use them in your printf() functions. However, you should use constants such as it from . Do not define a yourself. 2.1 Sine and Cosine The domain of sin and cos is (27, 27t), and so centering them around 0 makes sense. The Taylor series for sin(x) centered about Ois: sin(x) = [(-1) (2K+1)! ~ x2k+1 k=0 If we expand a few terms, then we get: x x13 sin(x)=x- x3 x5 x7 x x x x11 + 3! + 5! + 7! 9! 11! 13! + The series for cos(x) centered about O is: x2K cos(x)=[(-1), (2k)! k=0 If we expand a few terms, then we get: x2 x4 6 x8 x 10 cos(x)=1- + 4! 2! + 6! 8! x 12 +O(x+4). + 10! 12! 2.2 Tangent Unlike sin and cos, tan does not have a simple Taylor series expansion: oo (1)n-1221 (221 1 )B2n x2n-1, TT tan(x)= Ixl. Note that the function is named Sqrt(). It begins with an initial guess xo that it uses to compute better approximations. The square root is said to be calculated once the value converges, i.e. the difference between consecutive approximations is small. (Xk+ -). Computing Vx using Newton's method. 1 #define EPSILON 1e-9 2 3 static inline double Abs (double x) { 4 return x EPSILON) { 11 old = x_n; 12 x_n 0.5 * (x_n + y / x_n); 13 } 14 return x_n; 15 } Your function Log() should behave the same as log() from : compute In(x). The pro- cedure is very much the same as it was for the square root example, the main difference being that f(x)=y-ex, since ex is the inverse of In, i.e. In(e*) = x. Another key difference is the value converges when exi - y is small, where xi is initially 1.0 and is used to compute better approximations. In order to implement this function, you will have to use your Exp() function. Using the exp() function from 3 Command-line Options GUIs tend to impose a large overhead on every single piece of software, even the smallest, and this overhead completely changes the programming environment. Small utility programs are no longer worth writing. Their functions, instead, tend to get swallowed up into omnibus software packages. -Neal Stephenson, In the Beginning... Was the Command Line Your test harness will determine which implemented functions to run through the use of command- line options. In most C programs, the main() function has two parameters: int argc and char **argv. A command, such as ./hello argi arg2, is split into an array of strings referred to as arguments. The parameter argv is this array of strings. The parameter argc serves as the argument counter, the value in which is the number of arguments supplied. Try this code, and make sure that you understand it: Trying out command-line arguments. 1 #include 2 3 int main(int argc, char **argv) { 4 for (int i = 0; i with a test harness and output the results into a table similar to what is show in Figures 1 and 2. $ ./mathlib-test -s head -n 5 X Sin Library Difference -6.2832 -6.1832 -6.0832 -0.00000000 0.09983342 0.19866933 0.00000000 0.09983342 0.19866933 -0.0000000000 0.0000000000 -0.0000000000 Figure 1: First five lines of program output for sin. $ ./mathlib-test - head -n 5 Cos X Library Difference -6.2832 -6.1832 -6.0832 1.00000000 0.99500417 0.98006658 1.00000000 0.99500417 0.98006658 -0.0000000000 -0.0000000000 0.0000000000 Figure 2: First five lines of program output for cos. From left to right, the columns represent the input number, your program's cosine value from the input number, the actual math library's value from the input number and lastly, the difference between your value and the library's value. You will test sin and cos in the range [-271, 27t) with steps of 0.1, while tan will be tested in the range [-1/3,1/3) with steps of 0.1. ex and log will be tested in the range [1,10) with steps of 0.1. Since sin and cos are valid over the real numbers, you need to accept any valid double-which means you will need to renormalize the input-271s x s 27. You also want to do this so that your Taylor series converges rapidly. Each implementation will be a separate function. You must name the functions Sin, Cos, Tan, Exp, and Log. Since the math library uses sin, cos, tan, exp, and log, you will not be able to use the same names. You may not use any of the functions from in any of your functions. You may only use them in your printf() functions. However, you should use constants such as it from . Do not define a yourself. 2.1 Sine and Cosine The domain of sin and cos is (27, 27t), and so centering them around 0 makes sense. The Taylor series for sin(x) centered about Ois: sin(x) = [(-1) (2K+1)! ~ x2k+1 k=0 If we expand a few terms, then we get: x x13 sin(x)=x- x3 x5 x7 x x x x11 + 3! + 5! + 7! 9! 11! 13! + The series for cos(x) centered about O is: x2K cos(x)=[(-1), (2k)! k=0 If we expand a few terms, then we get: x2 x4 6 x8 x 10 cos(x)=1- + 4! 2! + 6! 8! x 12 +O(x+4). + 10! 12! 2.2 Tangent Unlike sin and cos, tan does not have a simple Taylor series expansion: oo (1)n-1221 (221 1 )B2n x2n-1, TT tan(x)= Ixl. Note that the function is named Sqrt(). It begins with an initial guess xo that it uses to compute better approximations. The square root is said to be calculated once the value converges, i.e. the difference between consecutive approximations is small. (Xk+ -). Computing Vx using Newton's method. 1 #define EPSILON 1e-9 2 3 static inline double Abs (double x) { 4 return x EPSILON) { 11 old = x_n; 12 x_n 0.5 * (x_n + y / x_n); 13 } 14 return x_n; 15 } Your function Log() should behave the same as log() from : compute In(x). The pro- cedure is very much the same as it was for the square root example, the main difference being that f(x)=y-ex, since ex is the inverse of In, i.e. In(e*) = x. Another key difference is the value converges when exi - y is small, where xi is initially 1.0 and is used to compute better approximations. In order to implement this function, you will have to use your Exp() function. Using the exp() function from 3 Command-line Options GUIs tend to impose a large overhead on every single piece of software, even the smallest, and this overhead completely changes the programming environment. Small utility programs are no longer worth writing. Their functions, instead, tend to get swallowed up into omnibus software packages. -Neal Stephenson, In the Beginning... Was the Command Line Your test harness will determine which implemented functions to run through the use of command- line options. In most C programs, the main() function has two parameters: int argc and char **argv. A command, such as ./hello argi arg2, is split into an array of strings referred to as arguments. The parameter argv is this array of strings. The parameter argc serves as the argument counter, the value in which is the number of arguments supplied. Try this code, and make sure that you understand it: Trying out command-line arguments. 1 #include 2 3 int main(int argc, char **argv) { 4 for (int i = 0; i

















