A warehouse, similar to Ocados algorithm-controlled warehouse that you met in The Secret Rules of Modern Living: Algorithms Part 3, has a despatch area and a vast storage area divided into zones. Requested items are brought to despatch from the storage area by an automatic picking system. An automated crate travels along tracks from despatch to the appropriate storage area zones, and back to despatch. Tracks are in pairs that allow the crate to travel in either direction.

The crate may need to pass through other zones to get to and from the zones where the requested items are.

The warehouse can be represented by a weighted digraph. Nodes represent the despatch and storage zones. Weighted edges represent tracks between the despatch and storage zones, and between zones. A weight represents the time (in seconds) that it takes to travel between the two zones joined by the edge.

Below is an instance of a weighted digraph that represents an example warehouse:

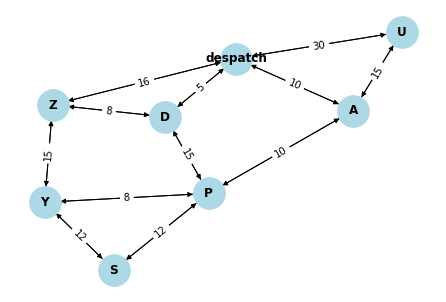
Question A:

Use Dijsktra's algorithm to compute the shortest path from despatch to each zone.

The code below is for your reference:

warehouse = WeightedDiGraph() warehouse.add_node('despatch') warehouse.add_node('A') warehouse.add_node('D') warehouse.add_node('P') warehouse.add_node('S') warehouse.add_node('U') warehouse.add_node('Y') warehouse.add_node('Z')

warehouse.add_edge('despatch','U',30) warehouse.add_edge('U','despatch',30) warehouse.add_edge('despatch','A',10) warehouse.add_edge('A','despatch',10) warehouse.add_edge('despatch','D',5) warehouse.add_edge('D','despatch',5) warehouse.add_edge('despatch','Z',16) warehouse.add_edge('Z','despatch',16) warehouse.add_edge('A','U',15) warehouse.add_edge('U','A',15) warehouse.add_edge('A','P',10) warehouse.add_edge('P','A',10) warehouse.add_edge('P','S',12) warehouse.add_edge('S','P',12) warehouse.add_edge('D','Z',8) warehouse.add_edge('Z','D',8) warehouse.add_edge('P','D',15) warehouse.add_edge('D','P',15) warehouse.add_edge('P','Y',8) warehouse.add_edge('Y','P',8) warehouse.add_edge('Y','S',12) warehouse.add_edge('S','Y',12) warehouse.add_edge('Y','Z',15) warehouse.add_edge('Z','Y',15)

warehouse.draw()

Question B:

Implement the shortest path between nodes algorithm below as a function in Python. Include a docstring. Make sure that your function inputs are in the order warehouse, start, end. We have provided the reverse_in_place() code.

Here is a definition of a function that, given a connected weighted digraph, finds the shortest path from a given start node to a given end node.

Function: shortest path between nodes Inputs: warehouse, a weighted digraph; start, a node; end, a node Preconditions: start and end are different nodes in warehouse; warehouse is connected Output: path, a sequence of nodes Postconditions: path is the shortest path from start to end in warehouse

Here is the description of an algorithm that solves the shortest path between nodes problem.

1-Use Dijkstra's algorithm to construct a tree of shortest paths from start to every other node of warehouse.

2-Let path be the sequence [end].

3-In the tree, starting with end visit the in-neighbour of the node, then the in-neighbour of that node, and so on, until getting to start, appending each node to path.

4-Reverse the sequence path using reverse_in_place()

Below are the reverse code and the testing code:

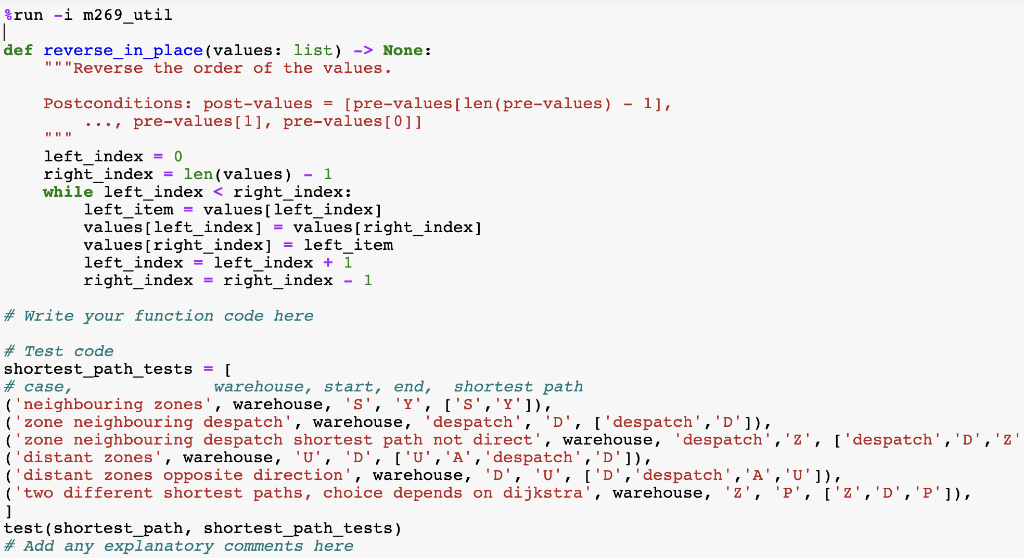
%run -i m269_util

def reverse_in_place(values: list) -> None: """Reverse the order of the values.

Postconditions: post-values = [pre-values[len(pre-values) - 1], ..., pre-values[1], pre-values[0]] """ left_index = 0 right_index = len(values) - 1 while left_index

# Write your function code here

# Test code shortest_path_tests = [ # case, warehouse, start, end, shortest path ('neighbouring zones', warehouse, 'S', 'Y', ['S','Y']), ('zone neighbouring despatch', warehouse, 'despatch', 'D', ['despatch','D']), ('zone neighbouring despatch shortest path not direct', warehouse, 'despatch','Z', ['despatch','D','Z']), ('distant zones', warehouse, 'U', 'D', ['U','A','despatch','D']), ('distant zones opposite direction', warehouse, 'D', 'U', ['D','despatch','A','U']), ('two different shortest paths, choice depends on dijkstra', warehouse, 'Z', 'P', ['Z','D','P']), ] test(shortest_path, shortest_path_tests) # Add any explanatory comments here