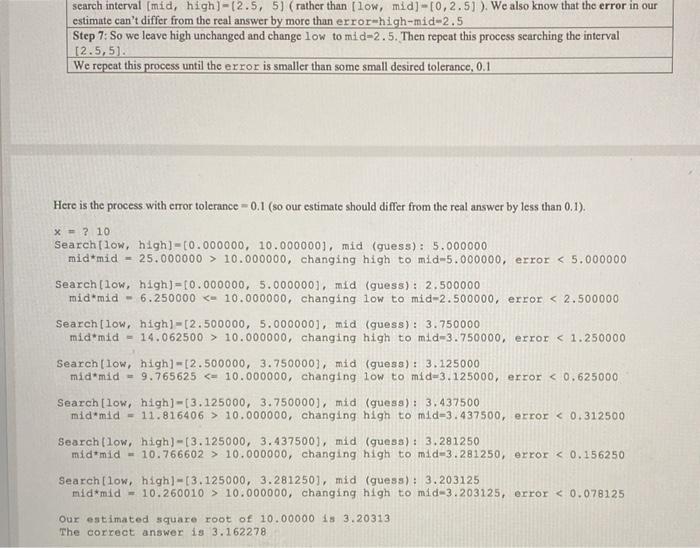
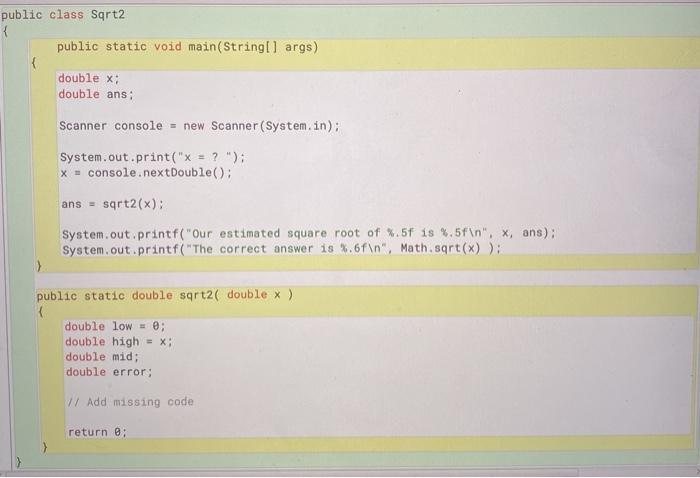
add missing code

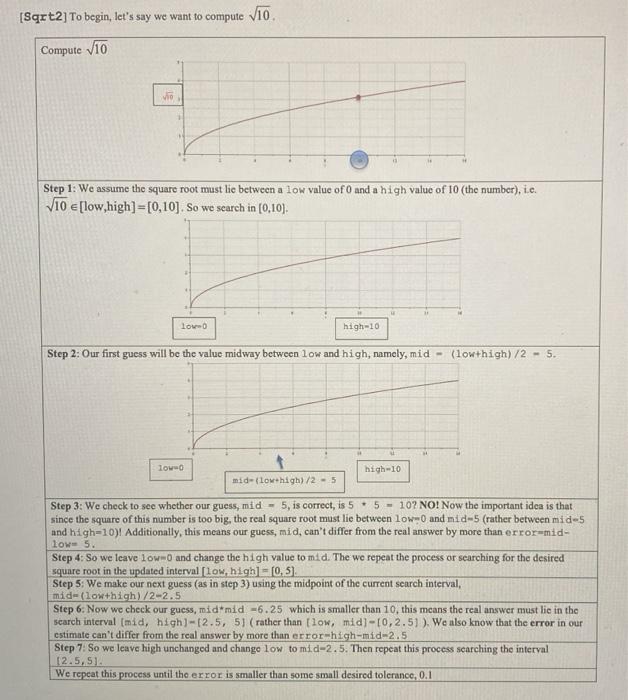
[Sqrt2) To begin, let's say we want to compute V10 Compute Vio Vio Step 1: We assume the square root must lie between a low value of 0 and a high value of 10 (the number), i.e. V10 [low,high]=[0,10). So we search in [0,10). low high-10 Step 2: Our first guess will be the value midway between low and high, namely, mid - (lowthigh)/2 - 5. lowo high-10 mid-flow high)/2 - 5 Step 3: We check to see whether our guess,mid - 5, is correct, is 5.5 - 102 NO! Now the important idea is that since the square of this number is too big, the real square root must lie between low- and mid-5 (rather between mid-5 and high-10) Additionally, this means our guess, mid, can't differ from the real answer by more than error=mid- low- 5. Step 4: So we cave low and change the high value to mid. The we repeat the process or searching for the desired square root in the updated interval [low, high] = [0,5). Step 5: We make our next guess (as in step 3) using the midpoint of the current search interval, mid-(low thigh)/2-2.5 Step 6. Now we check our guess, mid*mid -6.25 which is smaller than 10, this means the real answer must lie in the scarch interval (mid, high) - [2.5, 5] (rather than Clow, mid]-[0,2.51). We also know that the error in our estimate can't differ from the real answer by more than error-high-mid-2.5 Step 7: So we leave high unchanged and change low to mid-2.5. Then repeat this process searching the interval [2.5,51. We repeat this process until the error is smaller than some small desired tolerance, 0.1 search interval (mid, high]-[2.5, 51 (rather than low, mid]-[0,2.51). We also know that the error in our estimate can't differ from the real answer by more than error-high-mid-2.5 Step 7: So we leave high unchanged and change low to mid-2.5. Then repeat this process searching the interval [2.5,5). We repeat this process until the error is smaller than some small desired tolerance, 0.1 Here is the process with error tolerance - 0.1 (so our estimate should differ from the real answer by less than 0.1). X? 10 Search[low, high)-(0.000000, 10.000000), mid (guess): 5.000000 mid*mid - 25.000000 > 10.000000, changing high to mid-5.000000, error 10.000000, changing high to mid-3.750000, error 10.000000, changing high to mid=3.437500, error 10.000000, changing high to mid=3.281250, error 10.000000, changing high to mid-3.203125, error