Ah sudoku...a game that has been celebrated for a long time, now you all will get the chance to experience this simple yet complex game. The game of sudoku is traditionally played on a 9x9 board where each cell contains a number from 1 to 9. Seems simple but here is where it gets a bit complicated: you cannot have the same number on any row or column, and the real hard part is that there cannot be any duplicate number in all 9 3x3 sectors on the grid.

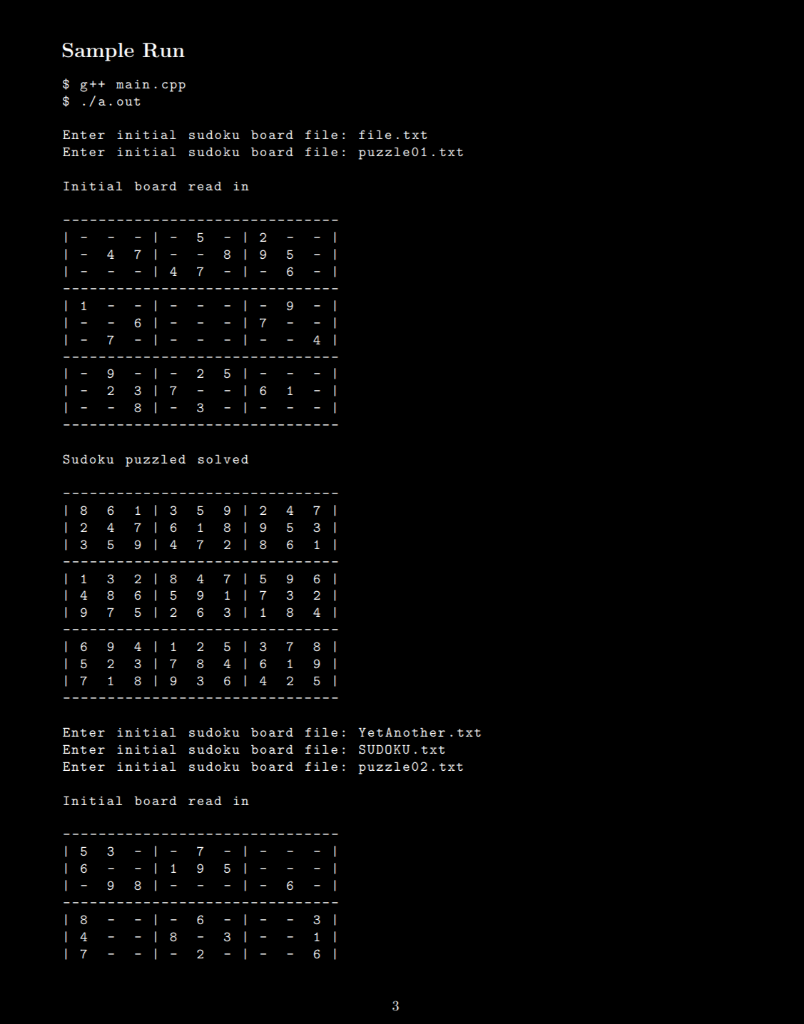
CS302 Assignment 2: Sudoku Solver SUDOKU Description Ah sudoku...a game that has been celebrated for a long time, now you all will get the chance to experience this simple yet complex game. The game of sudoku is traditionally played on a 9x9 board where each cell contains a number from 1 to 9. Seems simple but here is where it gets a bit complicated: you cannot have the same number on any row or column, and the real hard part is that there cannot be any duplicate number in all 9 3x3 sectors on the grid. 5 3 6 9 8 7 1 95 6 8 6 8 3 4 7 5 3 4 6 7 8 9 1 2 6 7 21 9 53 48 1 9 83 4 2/5 6 7 8 5 9 7 6 1 4 2 3 4 26 8 5 379 1 7 1 319 2 48 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 52 8 61 7 9 3 1 6 2 8 5 79 2 6 4 1 9 8 Figure 1: Initial Board Figure 2: Solved Board In figure 1, we have an initial sudoku board (this will be given as input to our program), and our program would need to fill out the blank spaces with numbers that solve the puzzle which is shown in figure 2. Notice the darker lines that separate each sector, so for example in the top left 3x3 sector, in figure 2, 4 is used in row 1 column 3, and no other cell in the sector uses 4, however in all other sectors, 4 appears once in each of them but they do not share a row or column in common. You can also find more information about sudoku using the following link https://en.wikipedia.org/wiki/Sudoku. You can also play the game to get a better idea if you want using the following link https://sudoku.com/. It will be your job to write a program that solves this, and don't worry, no linked lists to worry about this time, however you have to worry about everyone's favorite topic...recursion. Contents of main You will not need to worry about dynamic memory allocation since you know the size of the board and the size of each sector, the size of each sector, and the coordinates of each sector. You will first prompt the user for an input file that gives you the initial board, there will be 9 rows of integers and each row contains 9 integers 0-9 separated by a space, and each row is separated by a end of line character. The Os represent a blank spot on the board that would need to be filled out. You can assume that the input will be a valid initial sudoku board. Your program would need to print out the initial board and the solved board (see sample output) Backtracking Algorithm You would need to use a recursive backtracking algorithm which is a brute force method that literally tries ev- erything until a solution is finally found, I have paraphrased how you would approach this solution/recursive function: Each function call works on a cell on the board on coordinates [i, j] At the start of each function, you determine if the puzzle is already solved, you would return a true value which gets relayed through the series of already existing function calls on the system stack You check the cell to see if a non-blank exists at position [i, j] if it's a blank you recursively call the function and pass in new x and y coordinates in, and then simply return what that function call returns, i.e. you just relay (I recommend you row by row or column by column traversal) If the cell is blank, you pick a number to assign to the cell (maybe using a loop that ranges from 1 to 9), once a number chosen can be used, assign it to the cell and call the function recursively so the next cell is processed (pass in new x and y coordinates into the function), then based on what that function returns you do the following If true is returned, then you can conclude the puzzle is solved, return true If false is returned, then go back to the outer bullet above this sub bullet list but pick a different number this time around, if no such number can be used then return false to backtrack to the previous function which will force that function to pick a new number for its respective cell Input Prompt the user for the input file that contains the initial sudoku puzzle, if an invalid file is read then simply re-prompt, if the user enters NO then the program will stop accepting input and will terminate. Output For each input file, output the initial puzzle and then the solved puzzle below. Specifications Comment your code and your functions No global variables (global constants are ok) Must use a recursive backtracking algorithm, don't copy the iterative methods found online for reasons... 2 Sample Run $ g++ main.cpp $ ./a.out Enter initial sudoku board file: file.txt initial sudoku board file: puzzle01.txt Enter Initial board read in 5 5 12 8 19 7 5 6 14 7 1 9 6 17 7 | - 9 - | - 25 | - 23 7 |- - 8 - 3 1 Sudoku puzzled solved | 8 | 2 | 3 6 4 5 1 | 3 76 9 | 4 5 92 4 71 1 8 | 9 5 31 7 2 1 8 6 1 | 1 3 | 4 8 19 7 2 | 8 6 | 5 5 | 2 4 9 6 7 | 5 9 1 I 7 3 3 | 1 8 2 | 6 15 | 7 9 2 1 4 1 2 5 1 3 7 81 3 | 7 8 4 | 6 1 91 8 | 9 3 6 4 2 5 | Enter initial sudoku board file: Yet Another .txt Enter initial sudoku board file: SUDOKU .txt Enter initial sudoku board file: puzzle02.txt Initial board read in | 5 3 | 6 - |- 9 7 9 1 1 51 T 8 6 6 | 8 | 4 | 7 8 3 31 1 1 61 2 3 CS302 Assignment 2: Sudoku Solver SUDOKU Description Ah sudoku...a game that has been celebrated for a long time, now you all will get the chance to experience this simple yet complex game. The game of sudoku is traditionally played on a 9x9 board where each cell contains a number from 1 to 9. Seems simple but here is where it gets a bit complicated: you cannot have the same number on any row or column, and the real hard part is that there cannot be any duplicate number in all 9 3x3 sectors on the grid. 5 3 6 9 8 7 1 95 6 8 6 8 3 4 7 5 3 4 6 7 8 9 1 2 6 7 21 9 53 48 1 9 83 4 2/5 6 7 8 5 9 7 6 1 4 2 3 4 26 8 5 379 1 7 1 319 2 48 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 52 8 61 7 9 3 1 6 2 8 5 79 2 6 4 1 9 8 Figure 1: Initial Board Figure 2: Solved Board In figure 1, we have an initial sudoku board (this will be given as input to our program), and our program would need to fill out the blank spaces with numbers that solve the puzzle which is shown in figure 2. Notice the darker lines that separate each sector, so for example in the top left 3x3 sector, in figure 2, 4 is used in row 1 column 3, and no other cell in the sector uses 4, however in all other sectors, 4 appears once in each of them but they do not share a row or column in common. You can also find more information about sudoku using the following link https://en.wikipedia.org/wiki/Sudoku. You can also play the game to get a better idea if you want using the following link https://sudoku.com/. It will be your job to write a program that solves this, and don't worry, no linked lists to worry about this time, however you have to worry about everyone's favorite topic...recursion. Contents of main You will not need to worry about dynamic memory allocation since you know the size of the board and the size of each sector, the size of each sector, and the coordinates of each sector. You will first prompt the user for an input file that gives you the initial board, there will be 9 rows of integers and each row contains 9 integers 0-9 separated by a space, and each row is separated by a end of line character. The Os represent a blank spot on the board that would need to be filled out. You can assume that the input will be a valid initial sudoku board. Your program would need to print out the initial board and the solved board (see sample output) Backtracking Algorithm You would need to use a recursive backtracking algorithm which is a brute force method that literally tries ev- erything until a solution is finally found, I have paraphrased how you would approach this solution/recursive function: Each function call works on a cell on the board on coordinates [i, j] At the start of each function, you determine if the puzzle is already solved, you would return a true value which gets relayed through the series of already existing function calls on the system stack You check the cell to see if a non-blank exists at position [i, j] if it's a blank you recursively call the function and pass in new x and y coordinates in, and then simply return what that function call returns, i.e. you just relay (I recommend you row by row or column by column traversal) If the cell is blank, you pick a number to assign to the cell (maybe using a loop that ranges from 1 to 9), once a number chosen can be used, assign it to the cell and call the function recursively so the next cell is processed (pass in new x and y coordinates into the function), then based on what that function returns you do the following If true is returned, then you can conclude the puzzle is solved, return true If false is returned, then go back to the outer bullet above this sub bullet list but pick a different number this time around, if no such number can be used then return false to backtrack to the previous function which will force that function to pick a new number for its respective cell Input Prompt the user for the input file that contains the initial sudoku puzzle, if an invalid file is read then simply re-prompt, if the user enters NO then the program will stop accepting input and will terminate. Output For each input file, output the initial puzzle and then the solved puzzle below. Specifications Comment your code and your functions No global variables (global constants are ok) Must use a recursive backtracking algorithm, don't copy the iterative methods found online for reasons... 2 Sample Run $ g++ main.cpp $ ./a.out Enter initial sudoku board file: file.txt initial sudoku board file: puzzle01.txt Enter Initial board read in 5 5 12 8 19 7 5 6 14 7 1 9 6 17 7 | - 9 - | - 25 | - 23 7 |- - 8 - 3 1 Sudoku puzzled solved | 8 | 2 | 3 6 4 5 1 | 3 76 9 | 4 5 92 4 71 1 8 | 9 5 31 7 2 1 8 6 1 | 1 3 | 4 8 19 7 2 | 8 6 | 5 5 | 2 4 9 6 7 | 5 9 1 I 7 3 3 | 1 8 2 | 6 15 | 7 9 2 1 4 1 2 5 1 3 7 81 3 | 7 8 4 | 6 1 91 8 | 9 3 6 4 2 5 | Enter initial sudoku board file: Yet Another .txt Enter initial sudoku board file: SUDOKU .txt Enter initial sudoku board file: puzzle02.txt Initial board read in | 5 3 | 6 - |- 9 7 9 1 1 51 T 8 6 6 | 8 | 4 | 7 8 3 31 1 1 61 2 3