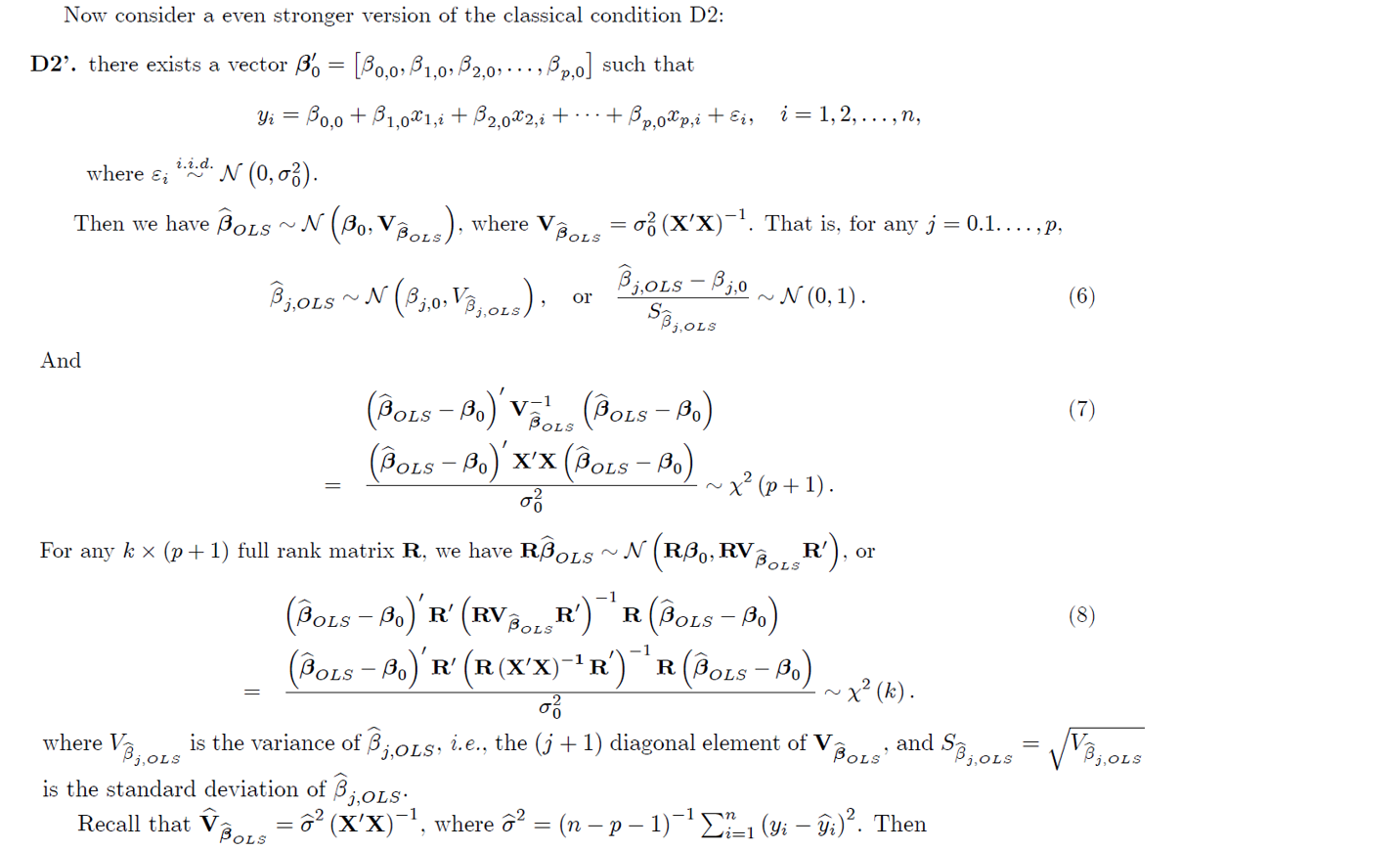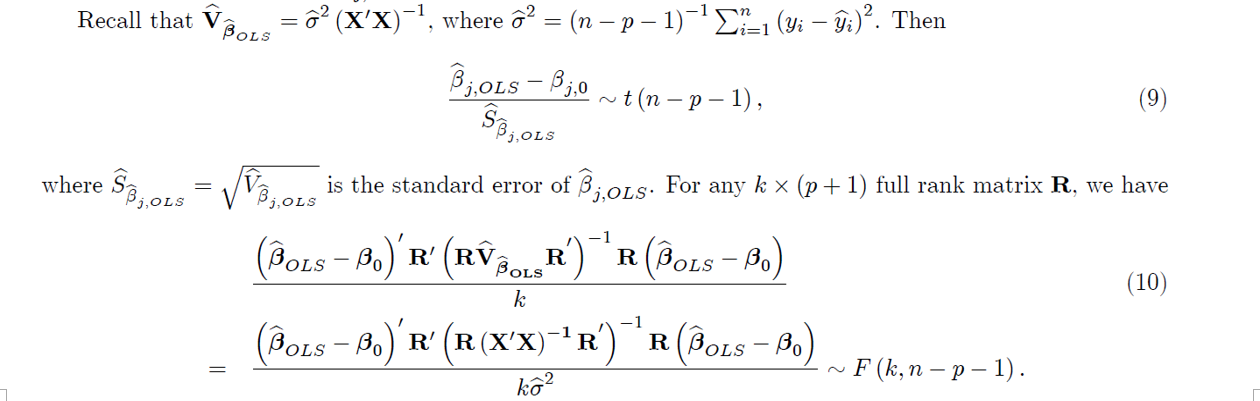ALL OF INFORMATION JUST ON THIS PICTURE.

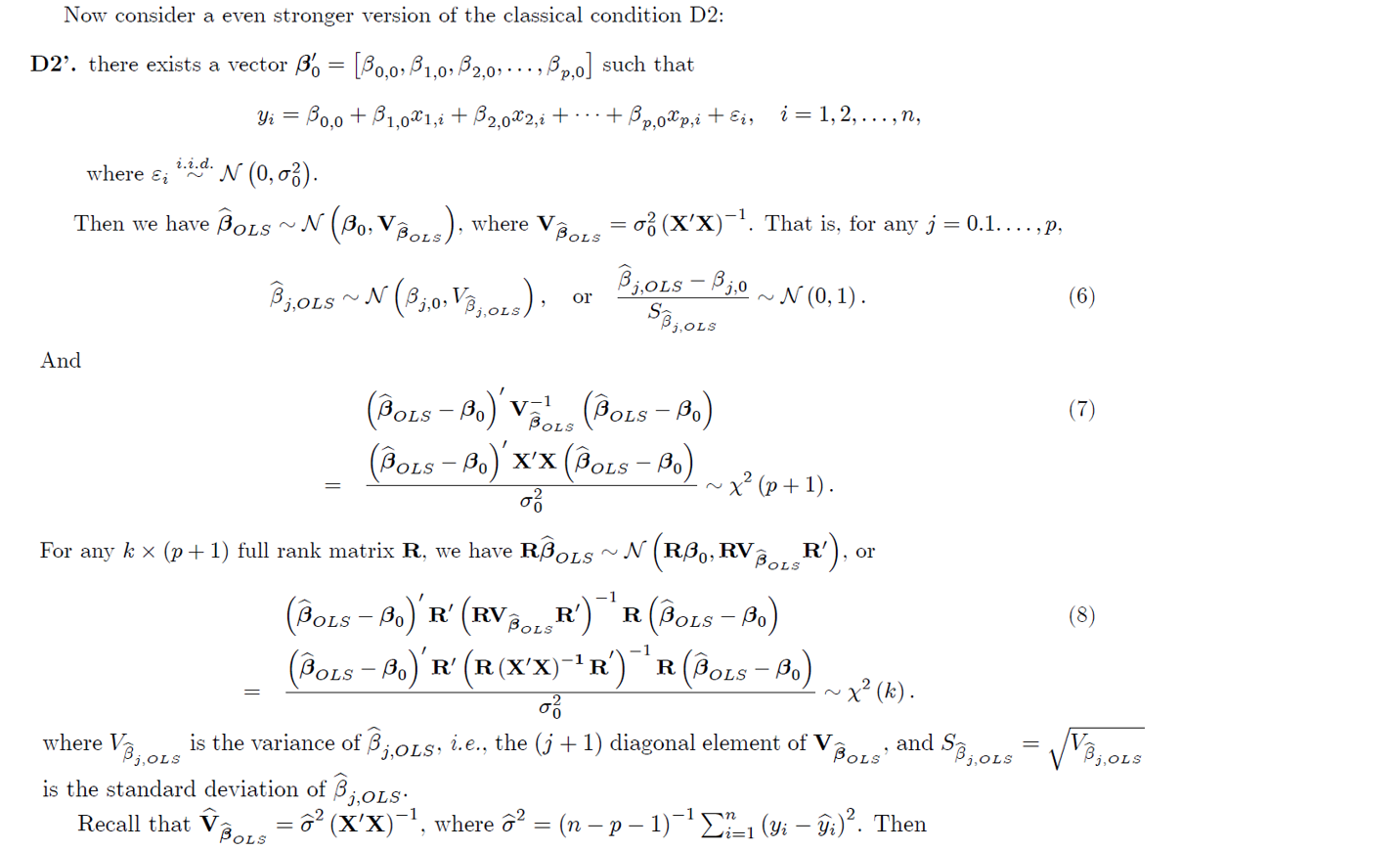
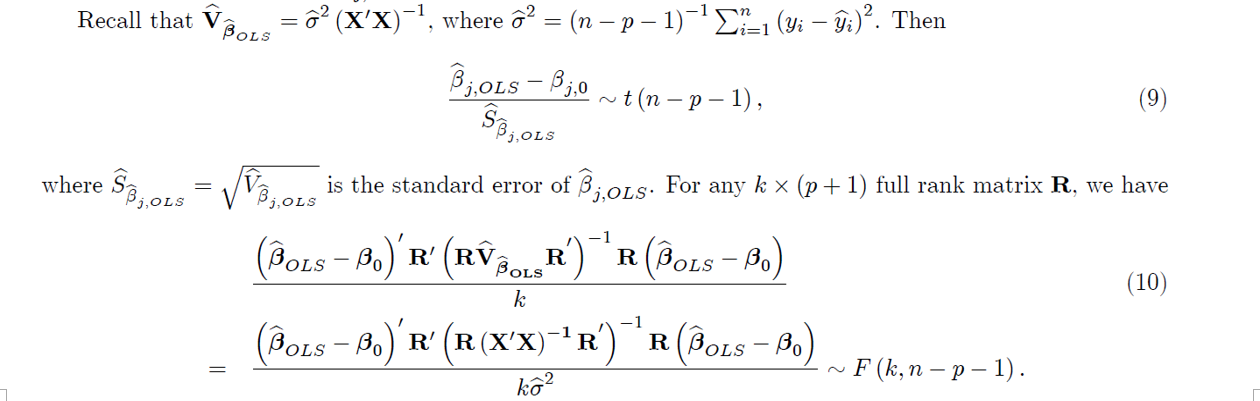
Consider the model: =1,2,...,n, (1) 2) Yi = x; 3+ u= Bo + B121,i + B2X2,i + ... + BpXp,i + Ui, where x; = [1, X1,1 , X2,1, . . . , Xp,i] and B' = [B0, B1, B2, ..., By], or y = XB+u, where y' = (y1, Y2, ..., yn], u' = [41, U2, ..., un], and x x'a Xp,2 X= 1 3p,1 1 1,1 21,2 X2,1 22,2 x, 21.n 22.n Xp,n Problem 1. For the multiple linear regression, suppose that 1 1 1 1 y = X= 28 4 7 6 9 8 2 x's 2 3 4 1 1 For this data matrix, can you calculate the ordinary least squares (OLS) estimator? Why or why not? Suppose that the OLS estimator Bols can be calculated. We know that Bols is an unbiased estimator for Bo, i.e., E (Bols) = Bo, when the following two classical conditions hold D1. {x1,1, X2,2, ..., Xp,i}=are nonstochastic, and D2. there exists a vector B = [B0,0,31,0, 32,0... , Bp,o] such that Yi = 30,0 + B1,081, i + 32,0X2,i +.... + Bp,0%p, i + Ein i=1,2,...,n, where E (@i) = 0, E (6) = o, and E (Eje;) = 0 for i, j = 1, 2, ..., n and i + j, Furthermore, under D1 and D2, Var (Bols) = Vots = of (X'X)"}, n 1 22 (yi i)? n- p - 1 i=1 is an unbiased estimator for om, and G (x'x)- BOLS (4) is an unbiased estimator for V BOLS' Problem 2. Consider the model: Yi = Bo + B1X1, + B2X2,i + Wig i = 1, 2, ...,n, Is Bols still an unbiased estimator for Bo when D1 and D2 hold in general but 1. E (6) = x, i, i.e., {ei} are not homoskedastic, but heteroskedastic? = 0 and B2,0 = 0, i.e., {21,1, X2,1}}=1 are not correlated with {yi}}=1? 3. there exists a vector B6 = [B0,0,1,0,B2,0] and + 0 such that 2. B1,0 70 Yi = Bo,o + B1,081, i + B2,0X2,i + YOX3,i + Ei, i=1,2,...,n, where {x3,i}}=1 are random variables such that E (23,i) = H3 + 0? For the model (1), let 9 = x3 LS Bools +B1,0L581,1 + 2,0LsX2,i + ... + Bp.ols@p,i be the fitted value for Yi, and j = Yi - i be the residuals. Recall that n Total sum of squares : TSS = (yi- 72, 2=1 n Regression sum of squares RSS = (3 - 9)?, and 2=1 n Error sum of squares ESS = (yi i)? Suz. i=1 Then Coefficient of determination: R2 = RSS TSS (5) Problem 3. Consider the following models: 1. For the model: Yi = a + Ui, i.e., we consider a model with only the intercept. What is the value of R2 ? 2. For the model: Yi = Bxi + Wis i.e., we consider a linear model of Xi without the intercept. Please show that TSS + RSS+ESS. That is, R2 = RSS/TSS may be negative. Now consider a even stronger version of the classical condition D2: D2'. there exists a vector B6 = [B0,0,31,0,B2,0, ..., Bp,o] such that B0,0 + $ 1,021,i + B 2,082,i + ... + Bp,o@p,i + Ei, Yi = i=1,2,...,n, 2.2.d. where si N (0,0). BOLS = o (X'X)-7. That is, for any j = 0.1....,P, Then we have Bols~N (Bo, Vozs), where V BjOLS ~N (8,0, Voc) B;,ols B3,0 ~ N (0,1). or SB3.0LS And (7) POLER'), O -1 (Bols - Bo)' VOLS (Bols Bo) (Pots B.)'x'x (Pols-Bo) ~x? (p+1). o For any k * (p+1) full rank matrix R, we have RBOLS ~ N (RB,, RV (Bols Bo)' r' (RV BOLS R') R(Bols - Bo) (POLS-B.) 'R' (R(X'X)-'R') R(BoLs - Be) ux (k). o is the variance of B;,ols, i.e., the (j +1) diagonal element of V and S8; 018 = 18,01$ is the standard deviation of Bjols: (XX)-, where d = (n - p - 1)^2 - (gi 9:). Then ~*(). where V2 Bj, OLS Bols? Recall that V BOLS Recall that V BOLS G (XX)-', where d = (n 1) -- (gi 9:). Then Bjols B3,0 ~t(n-p-1), (9) Sool j, OLS where $8,01$ 2,015 R BOLS is the standard error of Biols. For any k * (p+1) full rank matrix R, we have (Bols Bo)'R' (R R (Bols Bo) (10) (Bols Bo) R' (R (X'X)-'R' R (Bols - Bo F (k,n - p - 1). k2 k -1 Therefore, for any null hypothesis Ho : Rp. = c, we have the following test statistics: - 1 (RBOLS (RBOLS c) F c)' (RV c)' (R(X'X)-R R Bols k (11) -1 (RBOLS (RBOLS -c) ~ F (k, n p-1). ko2 For example, the null hypothesis, Ho : B0,1 = 30,2 : Bour = 0, can be written as Ho : Rp. =c, where 0 0 1 0 0 0 0 0 0 1 0 0 R= [0px1, Ip] = 0 0 0 1 and 0 C= = 0px1 0 O... 0 0 0 0 1 Problem 4. Consider the model: Yi = Bo + B181,i + B2X2,i + B3X3,i + B4X4,1 + 3585,i + ui, i=1,2,...,150. = c. Suppose that we have the following null hypotheses. Write out R and c in the form of Ho : RB. And write down the null distribution. : : 1. H41): 30,1 = 30,2 = 30,5 = 0. 2. H(2) : 30,0 + 330,3 630,4 = 4. 3. H3) : 30,2 + 430,4 +1 = = 230,12 4. HO4) : 30,0 + 330,1 + 30,3 + 530,5 = 7. Remark 1 For the null hypothesis Ho : 30,1 consider the following statistics: Bo,2 Bop = 0, another way to test the null is to RP / P (TSS ESS)/P F= (12) ESS/(n-p-1) (1 R2)/ (n - p - 1) This F statistic in equation (12) is numerically identical to the statistic in equation (11). We skip the details. Consider the model: =1,2,...,n, (1) 2) Yi = x; 3+ u= Bo + B121,i + B2X2,i + ... + BpXp,i + Ui, where x; = [1, X1,1 , X2,1, . . . , Xp,i] and B' = [B0, B1, B2, ..., By], or y = XB+u, where y' = (y1, Y2, ..., yn], u' = [41, U2, ..., un], and x x'a Xp,2 X= 1 3p,1 1 1,1 21,2 X2,1 22,2 x, 21.n 22.n Xp,n Problem 1. For the multiple linear regression, suppose that 1 1 1 1 y = X= 28 4 7 6 9 8 2 x's 2 3 4 1 1 For this data matrix, can you calculate the ordinary least squares (OLS) estimator? Why or why not? Suppose that the OLS estimator Bols can be calculated. We know that Bols is an unbiased estimator for Bo, i.e., E (Bols) = Bo, when the following two classical conditions hold D1. {x1,1, X2,2, ..., Xp,i}=are nonstochastic, and D2. there exists a vector B = [B0,0,31,0, 32,0... , Bp,o] such that Yi = 30,0 + B1,081, i + 32,0X2,i +.... + Bp,0%p, i + Ein i=1,2,...,n, where E (@i) = 0, E (6) = o, and E (Eje;) = 0 for i, j = 1, 2, ..., n and i + j, Furthermore, under D1 and D2, Var (Bols) = Vots = of (X'X)"}, n 1 22 (yi i)? n- p - 1 i=1 is an unbiased estimator for om, and G (x'x)- BOLS (4) is an unbiased estimator for V BOLS' Problem 2. Consider the model: Yi = Bo + B1X1, + B2X2,i + Wig i = 1, 2, ...,n, Is Bols still an unbiased estimator for Bo when D1 and D2 hold in general but 1. E (6) = x, i, i.e., {ei} are not homoskedastic, but heteroskedastic? = 0 and B2,0 = 0, i.e., {21,1, X2,1}}=1 are not correlated with {yi}}=1? 3. there exists a vector B6 = [B0,0,1,0,B2,0] and + 0 such that 2. B1,0 70 Yi = Bo,o + B1,081, i + B2,0X2,i + YOX3,i + Ei, i=1,2,...,n, where {x3,i}}=1 are random variables such that E (23,i) = H3 + 0? For the model (1), let 9 = x3 LS Bools +B1,0L581,1 + 2,0LsX2,i + ... + Bp.ols@p,i be the fitted value for Yi, and j = Yi - i be the residuals. Recall that n Total sum of squares : TSS = (yi- 72, 2=1 n Regression sum of squares RSS = (3 - 9)?, and 2=1 n Error sum of squares ESS = (yi i)? Suz. i=1 Then Coefficient of determination: R2 = RSS TSS (5) Problem 3. Consider the following models: 1. For the model: Yi = a + Ui, i.e., we consider a model with only the intercept. What is the value of R2 ? 2. For the model: Yi = Bxi + Wis i.e., we consider a linear model of Xi without the intercept. Please show that TSS + RSS+ESS. That is, R2 = RSS/TSS may be negative. Now consider a even stronger version of the classical condition D2: D2'. there exists a vector B6 = [B0,0,31,0,B2,0, ..., Bp,o] such that B0,0 + $ 1,021,i + B 2,082,i + ... + Bp,o@p,i + Ei, Yi = i=1,2,...,n, 2.2.d. where si N (0,0). BOLS = o (X'X)-7. That is, for any j = 0.1....,P, Then we have Bols~N (Bo, Vozs), where V BjOLS ~N (8,0, Voc) B;,ols B3,0 ~ N (0,1). or SB3.0LS And (7) POLER'), O -1 (Bols - Bo)' VOLS (Bols Bo) (Pots B.)'x'x (Pols-Bo) ~x? (p+1). o For any k * (p+1) full rank matrix R, we have RBOLS ~ N (RB,, RV (Bols Bo)' r' (RV BOLS R') R(Bols - Bo) (POLS-B.) 'R' (R(X'X)-'R') R(BoLs - Be) ux (k). o is the variance of B;,ols, i.e., the (j +1) diagonal element of V and S8; 018 = 18,01$ is the standard deviation of Bjols: (XX)-, where d = (n - p - 1)^2 - (gi 9:). Then ~*(). where V2 Bj, OLS Bols? Recall that V BOLS Recall that V BOLS G (XX)-', where d = (n 1) -- (gi 9:). Then Bjols B3,0 ~t(n-p-1), (9) Sool j, OLS where $8,01$ 2,015 R BOLS is the standard error of Biols. For any k * (p+1) full rank matrix R, we have (Bols Bo)'R' (R R (Bols Bo) (10) (Bols Bo) R' (R (X'X)-'R' R (Bols - Bo F (k,n - p - 1). k2 k -1 Therefore, for any null hypothesis Ho : Rp. = c, we have the following test statistics: - 1 (RBOLS (RBOLS c) F c)' (RV c)' (R(X'X)-R R Bols k (11) -1 (RBOLS (RBOLS -c) ~ F (k, n p-1). ko2 For example, the null hypothesis, Ho : B0,1 = 30,2 : Bour = 0, can be written as Ho : Rp. =c, where 0 0 1 0 0 0 0 0 0 1 0 0 R= [0px1, Ip] = 0 0 0 1 and 0 C= = 0px1 0 O... 0 0 0 0 1 Problem 4. Consider the model: Yi = Bo + B181,i + B2X2,i + B3X3,i + B4X4,1 + 3585,i + ui, i=1,2,...,150. = c. Suppose that we have the following null hypotheses. Write out R and c in the form of Ho : RB. And write down the null distribution. : : 1. H41): 30,1 = 30,2 = 30,5 = 0. 2. H(2) : 30,0 + 330,3 630,4 = 4. 3. H3) : 30,2 + 430,4 +1 = = 230,12 4. HO4) : 30,0 + 330,1 + 30,3 + 530,5 = 7. Remark 1 For the null hypothesis Ho : 30,1 consider the following statistics: Bo,2 Bop = 0, another way to test the null is to RP / P (TSS ESS)/P F= (12) ESS/(n-p-1) (1 R2)/ (n - p - 1) This F statistic in equation (12) is numerically identical to the statistic in equation (11). We skip the details