and tackling each part separately. This can help you identify where you are getting stuck and make it easier to find a solution.

DO ENTIRE QUESTIONs

Read the problem carefully: Before you start solving the problem, make sure you understand what it's asking. Read the problem carefully and make a note of any key words or phrases.

Identify the problem type: Determine what type of problem it is - algebraic, geometric, trigonometric, etc. Knowing the problem type will help you choose the appropriate formula or method to solve it.

Look for relevant information: Identify the given information in the problem that will help you solve it. Circle or underline the numbers or variables that are important.

Visualize the problem: Draw a diagram or graph to help you visualize the problem. This will help you better understand the problem and make it easier to solve.

Choose a strategy: Choose the appropriate strategy to solve the problem. Strategies include working backwards, guess and check, or using a formula.

Write out the equation: Write out the equation or formula you will be using to solve the problem. Make sure you have all the relevant variables and constants included.

Solve the equation: Solve the equation or formula you have written out. Follow the rules of arithmetic or algebraic operations to arrive at an answer.

Check your answer: Once you have arrived at an answer, double-check it to make sure it makes sense. Re-read the problem and check your calculations to avoid errors.

Round to the appropriate decimal place: If the problem asks for a specific decimal place, round your answer accordingly.

Label your answer: Make sure you label your answer with the appropriate unit of measurement or quantity. For example, if the problem asks for distance, label your answer in meters or feet.

Understand the problem: One of the most important steps in solving a math problem is to understand what the problem is asking you to do. Read the problem carefully and make sure you understand what is being asked. Look for keywords and phrases that indicate what operation(s) you need to perform to solve the problem. Identify any unknowns or variables that you will need to find or calculate.

Choose a strategy: Once you understand the problem, choose a strategy for solving it. There are many different strategies you can use, such as drawing a diagram, using algebraic equations, or working backwards. Choose a strategy that you are comfortable with and that is appropriate for the problem at hand.

Plan your solution: Before you start solving the problem, plan out your solution. This can include sketching a diagram, writing down any equations or formulas you will need to use, and breaking the problem down into smaller, more manageable parts. Planning your solution will help you avoid mistakes and make the problem easier to solve.

Show your work: When solving a math problem, it is important to show your work. Write down each step of the solution and show how you arrived at your answer. This not only helps you keep track of your progress, but also makes it easier to check your work and identify any mistakes you may have made.

Check your answer: After you have solved the problem, check your answer to make sure it is correct. Double-check your calculations and make sure you have answered the question that was asked. If you are using a calculator, make sure you have entered the numbers and operations correctly.

Practice: The more you practice solving math problems, the better you will become at it. Practice regularly by working through practice problems or completing assignments. This will help you build your skills and confidence in solving math problems.

Seek help when needed: If you are struggling to solve a math problem, don't be afraid to seek help. Talk to your teacher or a tutor, or join a study group to get help from your peers. There are also many online resources and forums where you can ask questions and get help from experts in the field.

Understand the concepts: To become proficient in solving math problems, it is important to have a solid understanding of the underlying concepts. Make sure you understand the basic principles of arithmetic, algebra, geometry, and other branches of math. This will make it easier to solve problems and will help you identify when you are making mistakes.

Be patient: Solving math problems can be challenging and frustrating at times. It is important to be patient and take your time when working through a problem. Rushing through a problem can lead to mistakes and errors, so take the time you need to work through each step carefully.

Practice critical thinking: Math problems often require critical thinking skills, such as analyzing information, making connections between different concepts, and identifying patterns. To become proficient in solving math problems, practice your critical thinking skills by working through complex problems and exploring different strategies for solving them.

Simplify the problem: If the problem seems overwhelming, try simplifying it by removing unnecessary information or breaking it down into smaller parts.

Use examples: Using examples can help you better understand the problem and come up with a solution.

Be organized: Keep your work organized and tidy, making it easier to double-check your calculations and identify any mistakes.

Practice good time management: Managing your time well can help you avoid rushing through the problem and making mistakes.

Read the instructions carefully: Make sure you understand any specific instructions or guidelines that are provided with the problem.

Identify patterns: Identifying patterns in the problem can help you come up with a solution more easily.

Look for shortcuts: Sometimes there are shortcuts or tricks to solving a math problem. Look for these and use them if possible.

Work with a partner: Working with a partner can help you solve problems more quickly and can also provide a different perspective on the problem.

Keep an open mind: Sometimes the solution to a problem may not be immediately obvious. Keeping an open mind and considering different approaches can help you find a solution.

Learn from your mistakes: If you mistake, don't get discouraged. Instead, use it as an opportunity to learn and improve your problem-solving skills.Break the problem down into smaller parts. If you are struggling to solve a problem, try breaking it down into smaller parts and tackling each part separately. This can help you identify where you are getting stuck and make it easier to find a solution.

Mathematics is the science and study of quality, structure, space, and change. Mathematicians seek out patterns, formulate new conjectures, and establish truth by rigorous deduction from appropriately chosen axioms and definitionsThere is debate over whether mathematical objects such as numbers and points exist naturally or are human creations. The mathematician Benjamin Peirce called mathematics "the science that draws necessary conclusions". Albert Einstein, on the other hand, stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."

Through abstraction and logical reasoning mathematics evolved from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records exist. Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Ele

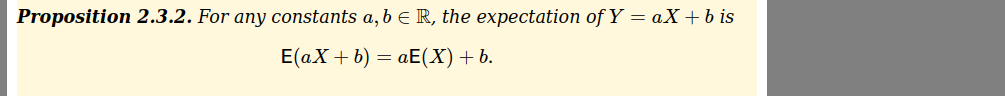
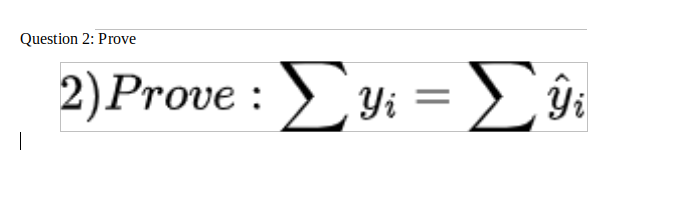
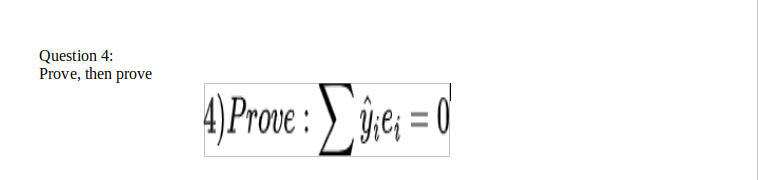
1. The conditional probability mass (density) function of X, given Y = y is defined as F for (x, y) = where f()) * 0 and fr() 2. The conditional probability mass (density) function of Y, given X = x is defined as T fxr (x, y) where fr (x) * 0. fx(x)Distribution with Expansions for Test of Hypothesis Test Statistic Degrees of Freedom Notations Difference between means of popu- X - HO *-distribution with X = Sample mean lation and sample (o unknown) v=n- 1 vn- 1 Difference between means of two (X - X2) t-distribution with = Population mean samples ( unknown) t= / 1 v=n, +n- 2 (a) If n, # n n2 (b) Ifn, =n, =n (*1 - X2) f-distribution with s = Sample standard t = v = 20 - 2 deviation n = Sample size V (n- 1) D = Degrees of freedom (c) n, = n, =n and the two samples d t-distribution with t= are not independent i.e., they are v=n-1 related in some way (This implies Vn- 1 that the pairs of observations (x, where d = x, - y y) belong to same sample unit d, = x, - y, and $2 = _ _(d, - a)] Equality of the population variances F-distribution with Note: Take the larger of the esti- F = v =n - 1 mates of variances of the samples Where of = [ ," ) of and a) - [me , )s? v2= n - 1 as of and the corresponding degrees of freedom as Population variance -distribution with v=n- 1 where 8 = (x -x] n21. Question Mark the correct alternative in each of the following: Let * he a binary aperatian on 0" defined by 3 '1' b = i for all a; b E 0+. The inverse of Ill i5 100 A. 105 a. 104 (2. ma D. none at theae \f\f\f12. Question Mark the correct alternative in each of the following: |Which of the following is true? 3+1) 8. A. * defined by a 14'13. : is a binary operation on Z a+b a. B. * defined by a \"1'1: : is a binary operation on Q C. a" binary commutative operations are associative D. Subtraction is a binary operation on N \f\f\f6. Question Mark the correct alternative in each of the following: If a binary' operation * is. defined on the set 2 of integere as a * h = 3a - b, then the value of {2 * 31*4 is A. 2 5.3 {2.4 [1.5 \f\f\fB. Question Mark the correct alternative in each of the following: X , where x E R - {El}; then the identity element with respect X If G is the set of all matrices of the form[ x x to the multiplication of matrices as binary operation, is 1 1 A. -1 1: 11!\": 1':' E. i 1: 1*2 '1': 132' C. 1-\": 1:2' :1 _1c D. \f\fQ5 : The radius of a circle is increasing at the rate of ll? cmfs. What is the rate of increase {if its circumference? \fQuestion 4: .3? '. 2 ". Find the values of x and y 50 that the vectors 4 +31 and .n +-"1 are equal idea is to use the graph) and invite others in your group to solve f(;l':) g 0. Respond to one or two other posts with clear solutions. Include information about key characteristics that you observe about x}. Use appropriate interval and set notation. Question 16: Find the position vector of the mid point of the vectorjoining the points P (2, 3, 4) and Q (4-, 1, - 2). \fProposition 2.3.2. For any constants a, b E R, the expectation on 2 (IX + b is E(aX + b) = aE{X) + b. \fL Question 1: Prove that sum of residuals in any regression model that contains an intercept b is always 0 1) Prove : Dei = _(yi - Di) = 0\f\f\fQuestion 7: Solve the following The PDF of a random variable X is 104:x30 10 0 otherwise What is P(X 1 (x - D) Solution