Answer appropriately
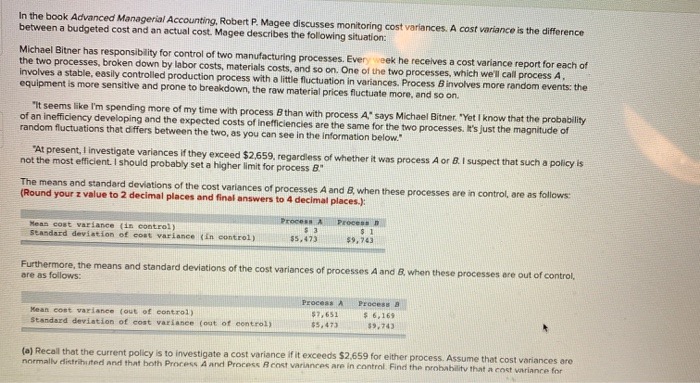
In the book Advanced Managerial Accounting, Robert P. Magee discusses monitoring cost variances. A cost variance is the difference between a budgeted cost and an actual cost. Magee describes the following situation: Michael Bitner has responsibility for control of two manufacturing processes. Every week he receives a cost variance report for each of the two processes, broken down by labor costs, materials costs, and so on. One of the two processes, which we'll call process A, involves a stable, easily controlled production process with a little fluctuation in variances. Process 8 involves more random events: the equipment is more sensitive and prone to breakdown, the raw material prices fluctuate more, and so on." "It seems like I'm spending more of my time with process # than with process A" says Michael Bitner. "Yet I know that the probability of an inefficiency developing and the expected costs of inefficiencies are the same for the two processes. It's just the magnitude of random fluctuations that differs between the two, as you can see in the Information below." "At present, I investigate variances if they exceed $2,659, regardless of whether it was process A or 8. I suspect that such a policy is not the most efficient. I should probably set a higher limit for process 8." The means and standard deviations of the cost variances of processes A and 8, when these processes are in control, are as follows: (Round your z value to 2 decimal places and final answers to 4 decimal places.): Process A Process n Mean cost variance (in control) $ 3 $ 1 Standard deviation of cost variance ( In control) $5.473 $9, 743 Furthermore, the means and standard deviations of the cost variances of processes A and 8, when these processes are out of control, are as follows: Procons A Process B Mean cost variance (out of control) $7, 651 $ 6, 161 Standard deviation of cost variance (out of control) #5,471 49,743 (a] Recall that the current policy is to investigate a cost variance if it exceeds $2,659 for either process. Assume that cost variances are normally distributed and that both Process A and Process A cost variances are in control Find the probability that a cost variance forTo investigate the effectiveness of a diet, a random sample of 16 female patients is drawn from a population of adult females using the diet. The weight of each individual in the sample is taken at the start and at the end of the diet. Assume that the population of differences in weight before and after the diet follows a normal distribution. Suppose the mean decrease in weights over all 16 subjects in the study is 4.0 pounds with the standard deviation of differences computed as 6.4 pounds. Let ux - jy = mean weight before the diet - mean weight after the diet. What conclusion can be made about the effectiveness of the diet, based on the test, at the 0.05 level of significance? The diet is not effective. O The diet is effective. O The sample size is relatively small to make a conclusion. O A conclusion cannot be drawn without calculating the p-value