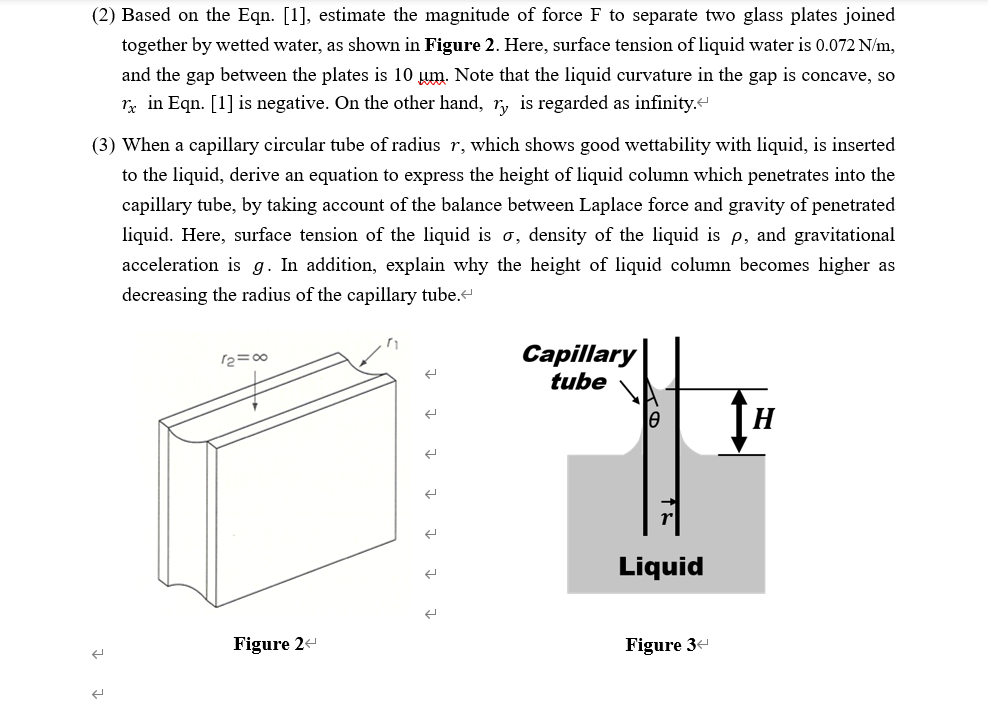
Answer the questions below about the effect of surface properties on materials processing. The "Laplace force", which acts to liquid as inner pressure to minimize surface area (or total surface excess energy), is represented by the following equation: P=(rx1+ry1); where is surface tension of a liquid, rx and ry are radius of curvature (in x-or y-plane). (1) First, we consider a microscopic area of a droplet to derive the Equation [1]. Fill the blanks (i) and (ii) with an appropriate expression using variables as defined below or in Figure 1. Note that surface tension is constant regardless of surface area. When the droplet expands by changing radius of curvature as rx+dr and rxrX+dr, the change of surface area could be expressed as follows: dA=(r1+dr)1(r2+dr)2rxxryy Then, the change of surface excess energy by the expansion droplet is expressed by the following: G=dA=. In contrast, the change of volume of microscopic area is approximately expressed as the volume of rectangular with initial surface area as bottom area and height of dr, as follows: In contrast, the change of volume of microscopic area is approximately expressed as the volume of rectangular with initial surface area as bottom area and height of dr, as follows: dV If inner pressure P acts to resist the expansion, the work to expand the droplet is represented by the following equation: W=PdV=P If we assume that the change of surface excess energy (G) is balanced with the work for expansion (W), the following relationship is derived by the combining Eqs.[3] and [5]: .=P. Finally, we can derive the Eqn. [1] by changing the shape of Eqn. [6]. (2) Based on the Eqn. [1], estimate the magnitude of force F to separate two glass plates joined together by wetted water, as shown in Figure 2. Here, surface tension of liquid water is 0.072N/m, and the gap between the plates is 10m. Note that the liquid curvature in the gap is concave, so rx in Eqn. [1] is negative. On the other hand, ry is regarded as infinity. (3) When a capillary circular tube of radius r, which shows good wettability with liquid, is inserted to the liquid, derive an equation to express the height of liquid column which penetrates into the capillary tube, by taking account of the balance between Laplace force and gravity of penetrated liquid. Here, surface tension of the liquid is , density of the liquid is , and gravitational acceleration is g. In addition, explain why the height of liquid column becomes higher as decreasing the radius of the capillary tube. Figure 3