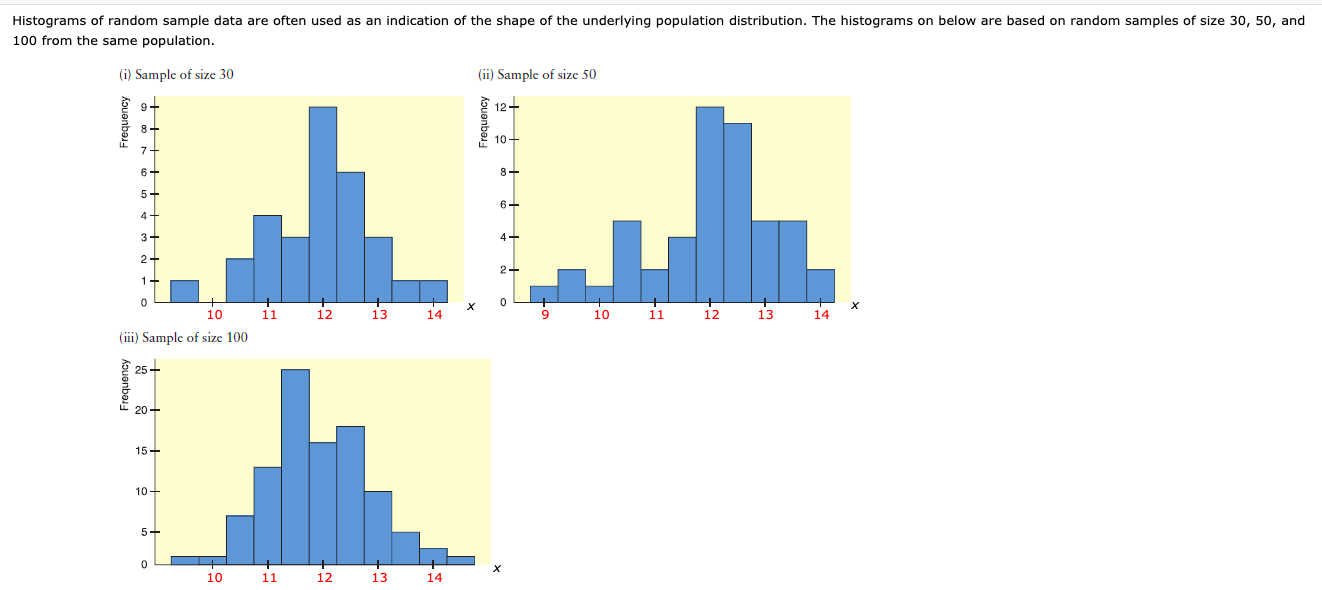
Any help explaining this would be greatly appreciated. I am a little confused about how to figure out the answer to part (b) of the question. If you could please explain HOW to get to the answer. Thank you.
(a) Using the midpoint labels of the three histograms, what would you say about the estimated range of the population data From smallest to largest? Complete the table giving the range of the sample data In each of the histograms. Smallest Value Largest value Histogram (I) Histogram (II) Histogram (Ill) Based on the completed table, select the most reasonable estimate of the range of the population data. C. 9 to 14 (j. 11 be 13 C. 9 to 15 (j. 9.5 to 14 .910 be 15 Does the bulk of the data seem to be between 10 and 14 in all three histograms? 1'\" Since there are many values outside the range 10 to 14, we can say that the bulk of the data is not between 10 and 14. 1'\" Since there are very few values outside the range 10 to 14Ir we can say that the bulk of the data is between 10 and 14. 1'\" Since there are no values outside the range 10 to 14Ir we can say that the bulk of the data is between 10 and 14. 1'\" Since there are very few outside the range 10 to 14, we can say that the bulk of the data is not between 10 and 14. 1'\" Since there are many values outside the range 10 to 14, we can say that the bulk of the data is between 10 and 14. (b) The population distribution from which the samples were drawn is symmetric and mound-shaped, with the top of the mound at 12, 95% of the data between 10 and 14, and 99.7% of the data between 9 and 15. How well does each histogram reect these characteristics? (Round your answers to one decimal place.) The three histograms 439017 6 mound-shaped and the data gradually reduces on either side of the mound in fashion. The highest bar in histogram (I) is at a value of x of unim. The highest bar In histogram {ii} is at a value ofx of units. The highest bar In histogram (Iii) is at a value ofx of units. So, the average top of the mound be said to be at a value ofx of approximater 12 units. In histogram (i), % of the sample data is between 10 and 14 inclusive, and '54: of the sample data ls between 9 and 15 inclusive. In histogram (ii), % of the sample data is between 10 and 14 inclusive. and % of the sample data is between 9 and 15 inclusive. In histogram (iii)r % of the sample data is between 1!) and 14 inclusive, and % of the sample data is between 9 and 15 inclusive. So, it reasonable to say that 99.7% of population distribution data is between 9 and 15. Finally, the bulk of the sample data between 10 and 14. So, it reasonable to say that 95% of the population distribution data is between 10 and 14. Histograms of random sample data are often used as an indication of the shape of the underlying population distribution. The histograms on below are based on random samples of size 30, 50, and 100 from the same population. (i) Sample of size 30 (ii) Sample of size 50 Frequency Frequency 12 - 10 8- 6- 4- 2- 10 11 12 13 14 X 10 11 12 13 14 X (iii) Sample of size 100 Frequency 25 - 20 - 15- 10- 5- 10 11 12 13 14 X