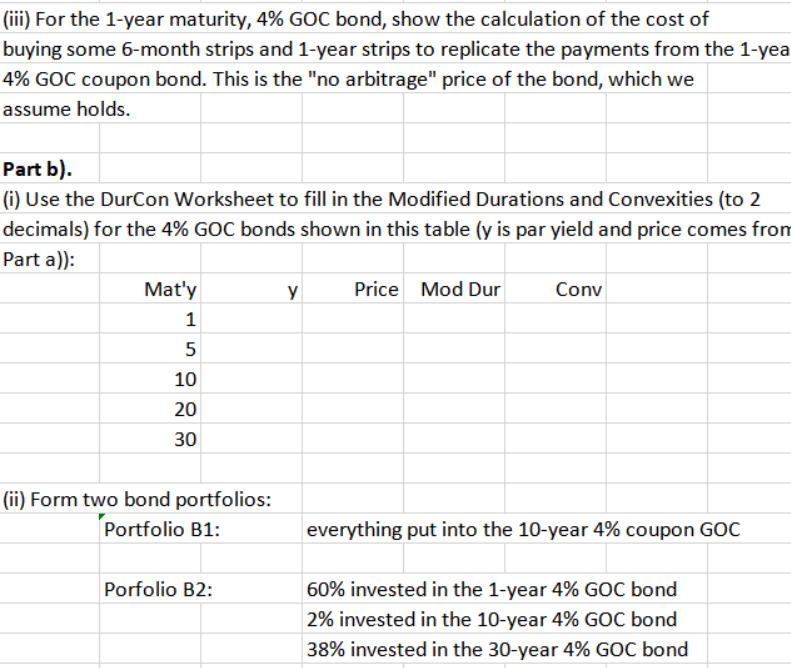
assume that all GOC bond's maturities are "t" on "curve" tab and the GOC's coupon rate is 4%; this is an annual rate that is paid every 6 months (i.e., paid at 2% per each 6 months). Finally, we will assume that the price of the GOC today can be determined from its par yield. Thus the par yield curve shown is to be taken as the GOC coupon bond curve for the exercise, and all those GOC bonds have 4% coupons. Part a). (i) Using either the Excel Pricing functions or the DurCon worksheet, use the par yields to get prices (to 3 decimals) of the 4% coupon GOC bonds with maturities of 1, 5, 10, 20 and 30 years. Fill in this table: Mat'y 1 5 10 20 30 y Price (ii) Why is the 30-year 4% GOC bond's par yield less than the 30-year strip rate (i.e., the yield on a 0% GOC 30-year bond)? (iii) For the 1-year maturity, 4% GOC bond, show the calculation of the cost of buying some 6-month strips and 1-year strips to replicate the payments from the 1-yea 4% GOC coupon bond. This is the "no arbitrage" price of the bond, which we assume holds. Part b). (i) Use the DurCon Worksheet to fill in the Modified Durations and Convexities (to 2 decimals) for the 4% GOC bonds shown in this table (y is par yield and price comes from Part a)): Mat'y 1 5 10 20 30 (ii) Form two bond portfolios: Portfolio B1: Porfolio B2: y Price Mod Dur Conv everything put into the 10-year 4% coupon GOC 60% invested in the 1-year 4% GOC bond 2% invested in the 10-year 4% GOC bond 38% invested in the 30-year 4% GOC bond Calculate the Modified Durations and Convexities of the two portfolios, B1 and B2. Take each number to 2 decimals. Comment on the similarities and differences between portfolios B1 and B2. (iii) Write down the Taylor's Series expected return equation ("dP/P") shown on page 2 of the course notes on Volatility, inserting the values for D (modified duration) and C (convexity) from part (ii). What is the major difference between B1 and B2? Give a simple numerical example. Part c). (i) Use the KRD Worksheet to fill in the three Key Rate Durations (to 3 decimals) for the 4% GOC bonds shown in this table (y is par yield and price comes from Part a)): Mat'y 1 5 10 20 30 y Price KRD(.5) KRD(10) KRD(30) (ii) Form two bond portfolios: Portfolio B1: Porfolio B2: everything put into the 10-year 4% coupon GOC 60% invested in the 1-year 4% GOC bond 2% invested in the 10-year 4% GOC bond 38% invested in the 30-year 4% GOC bond Calculate the three KRDs for each of the two portfolios, B1 and B2. Take each number to 3 decimals. Comment on the similarities and differences between B1 and B2. (iii) Write down the expected return equation shown on page 15 of the course notes on Volatility, inserting the KRD values for both B1 and B2. Part d). Assume a benchmark portfolio that is composed of equal (25%) weights in each of: Bond GOC 4% 1-Yr tenor GOC 4% 5-Yr tenor GOC 4% 10-Yr tenor GOC 4% 30-Yr tenor (i) For the benchmark portfolio, calculate the portfolio Modified Duration, Convexity and KRDs. (ii) Using the Taylor's Series Expected return equation on page Vol-2, what will be the expected return if all yields jump up by 1% (i.e., dy=0.01)? (iii) If the yield curve steepened: dhat r(.5) = -.0005, dhat (r10) =+.005 and dhat r(30) = +.01, what would be the benchmark return?