Question
Assume the production function can be written as: ( ) d 1 y Lan L hA ? ? ? ?? = ? ? ? ?
Assume the production function can be written as: ( ) d 1 y Lan L hA ? ? ? ?? = ? ? ? ? where h=human capital, LAND=the amount of land in the economy, A=productivity, y=income per-capita, and L=population. This economy has no physical capital. Land is in fixed supply. Assume h and A each grow at an exogenous positive rate and the parameter ? in the production function is positive and less than zero.
A. From this equation and the mathematical rules for growth rates we have discussed in class, derive the equation for the growth rate of y in terms of parameters and variables that are growing exogenously.
B. Assume the population growth rate is endogenously given by: L 0 1 g y = + ? ? , where ?0 and ?1 are positive parameters, based on the assumption that higher income per-capita induces a family to have more children. Prove that y eventually reaches a steady state (the level). Carefully explain using the equation(s) and/or graph(s) needed to prove your point. Do you need to make any additional assumptions about the parameters, or functions of the parameters, in the model to ensure a steady state for y obtains?
C. What is the steady state value for y in this model in terms of the parameters and the growth rates of productivity and of human capital? Do you need to make any additional assumptions about the parameters, or functions of the parameters, in the model to ensure a positive steady state for y obtains?
D. What is ss L g (steady state population growth) in terms of the parameters and the growth rates of productivity and of human capital?

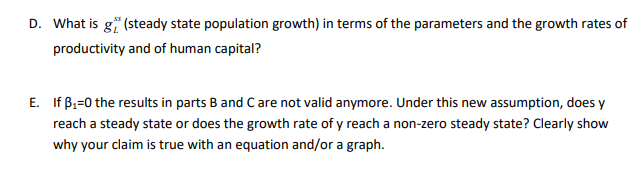
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


