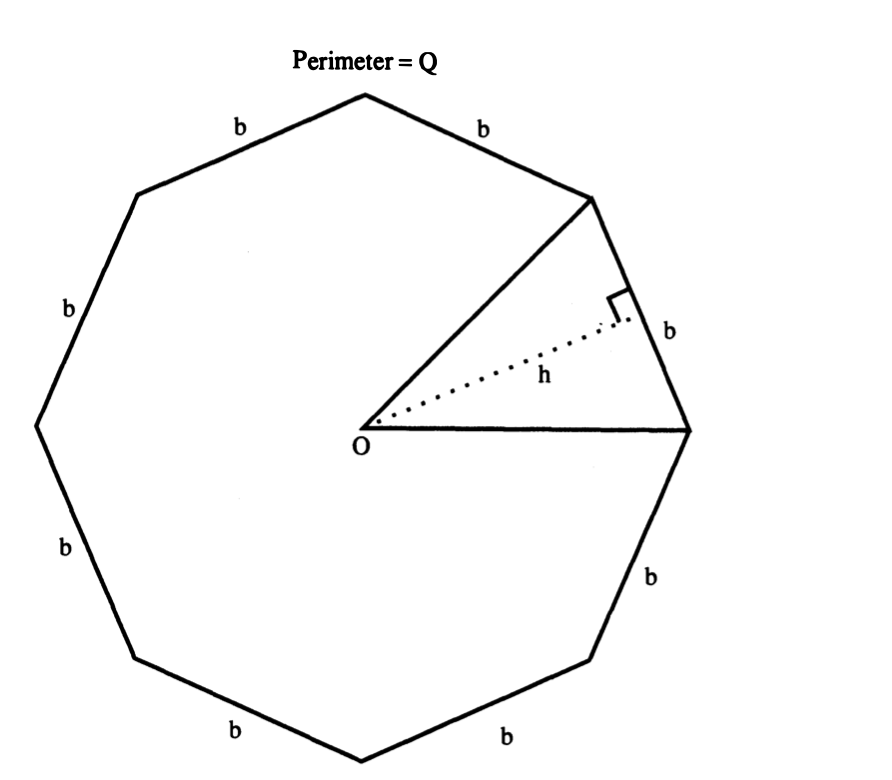
Assume the usual formula for the area of a circle of radius r: A = ?r^2 . Let ? be an arbitrary positive number. Calculate how big n must be so that the difference in area of the circle of radius r and the area of an inscribed (regular) n-gon whose side length is b is less than ?. Your answer should be an inequality of the form > with only n on the left side of >, and the constant ? and (only) the variables r, ?, and b on the right side of > (and no h). (Note: your answer you should show before your inequality how b, h and r are related. This is why the right hand side of your inequality should not contain the variable h).

Perimeter = Q b b b b O b b b b