Question
Assume you are buying a home between $100,000 and $400,000 in Texas. Assume a price that has not been chosen by another student; for example
Assume you are buying a home between $100,000 and $400,000 in Texas. Assume a price that has not been chosen by another student; for example if a student has chosen a $300,000 home price then no other student should choose a $300,000 home. Assume you borrow 80 % of the purchase price at 3.75 % interest rate. Assume interest and principal are paid annually, at the end of each year for 15 years. This will be a 15-year loan.
- What is your annual payment?
- What is the loan balance after 4 years?
- How much total payment you have made after 4 years?
- Suppose at the end of year 2 you spend $5,000 and at the end of year 3 you spend another $6,000 for the upkeep of your home. Suppose at the end of year 4 you sell your home at 30 % above the purchase price. What is the NPV of your home investment? Use a 3.75% discount rate. The NPV of your investment?
Hint: Look at my lecture notes of chapter 5 on page 15, in my lecture notes, it is monthly mortgage payment but here it is annual payment of mortgage. You need to draw a timeline:
Zero -----------Year 1Year2Year 3Year 4.
Then place cash outflows and cash inflows in the above timeline and then estimate NPV.
Below is the example that was provided.
Example from the textbooks authors: (Very good example, try to solve it before seeing the solution):
You wish to purchase a $170,000 home. You are going to put 10% down, so the loan amount will be $153,000 at 7.75% APR (.6458333333% per month = 7.75%/12), with monthly payments for 30 years. How much will each payment be? How much interest will you pay over the life of the loan? How much is owed at the end of year 20? How much interest will be paid in year 20? We could prepare a 360-month amortization schedule and while this is fairly straightforward in a spreadsheet or with various online calculators, there is an alternative way to answer the questions. Find the payment: PV = 153,000; N = 360; I/Y = 7.75/12; CPT PMT = 1,096.11 Find the total interest cost: Interest paid = total payments principal = 360(1,096.11) 153,000 = 241,599.60 Students are often amazed at how much interest is paid on a 30-year mortgage. The outstanding balance of the loan at any time equals the present value of the remaining payments. So, after 20 years, there are 120 payments remaining and the outstanding balance equals: PMT = -1,096.11; N = 120; I/Y = 7.75/12; CPT PV = 91,334.41 Students are also surprised to find that after making 2/3 of the payments, 60% of the principal remains unpaid. The interest paid in any year is equal to the sum of the payments made during the year minus the change in principal. After 228 months (19 years), the outstanding loan balance is $97,161.79. The change in principal is 97,161.80 91,334.41 = 5,827.39. Total interest paid in year 20 = 12(1,096.11) 5,827.39 = $7,325.93.
The above example is also solved in the Excel file for chapters 4&5.
The followings are taken from the authors lecture notes:
Loan Types and Loan Amortization
- Pure Discount Loans
- pays a single lump sum (principal and interest) at maturity. Treasury bills are a common example of pure discount loans.
Pure Discount Loans
- Interest-Only Loans
- pays only the interest each period and then pays the entire principal at maturity. Corporate bonds are a common example of interest-only loans.
- Amortized Loans
- repays part or all of principal over the life of the loan. Two methods are (1) fixed amount of principal to be repaid each period, which results in uneven payments, and (2) fixed payments, which results in uneven principal reduction. Traditional auto and mortgage loans are examples of the second type of amortized loans.
Use Excel and solve all the above examples. If in Excel you find the same answers, then you will do very well in your exams and homework.
Example from textbooks power points:
FUTURE VALUE: Multiple uneven Cash Flow
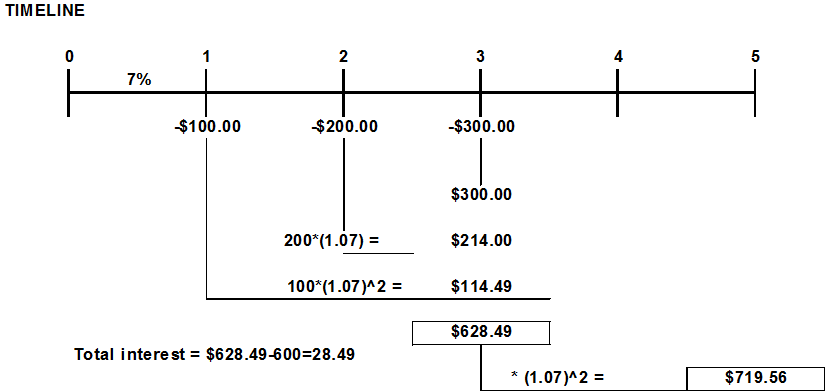
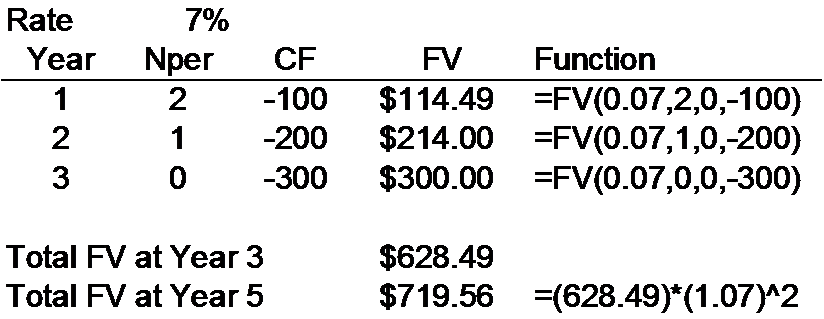
Another example:
- Suppose you invest $500 in a mutual fund today and $600 in one year.
- If the fund pays 9% annually, how much will you have in two years?
FV = $ 500 x (1.09)2 = $ 594.05
+ $ 600 x (1.09) = $ 654.00
= $1,248.05
You want to receive $5,000 per month in retirement. If you can earn .75% per month and you expect to need the income for 25 years, how much do you need to have in your account at retirement?
- N Months
- I/Y Monthly rate
- PMT Monthly Payment
- FV
- PV= $559,808.11
EXCEL: PV(.0075,300,5000,0)= $559,808.11
Example:
- Suppose you want to borrow $20,000 for a new car.
- You can borrow at 8% per year, compounded monthly (8/12 = .66667% per month).
- If you take a 4-year loan, what is your monthly payment?
EXCEL=PMT(.00667,48,20000,0)=$488.26
Example:
- Suppose you borrow $2,000 at 5% and you are going to make annual payments of $734.42. How long before you pay off the loan?
EXCEL: NPER(0.05,-734.42,2000,0) = 3 years
Example:
- Suppose you begin saving for your retirement by depositing $2,000 per year in an IRA. If the interest rate is 7.5%, how much will you have in 40 years?
EXCEL: =FV(0.075,40,-2000,0)=$454,513.04
Mathematic solution:
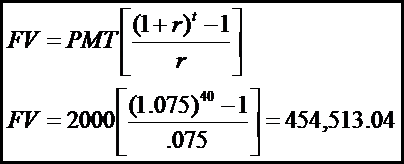
Example:
- You want to have $1 million to use for retirement in 35 years. If you can earn 1% per month, how much do you need to deposit on a monthly basis if the first payment is made in one month?
EXCEL: = PMT(0.01,420,0,1000000) = $155.50
Example
- You want to have $1 million to use for retirement in 35 years. If you can earn 1% per month, how much do you need to deposit on a monthly basis if the first payment is made today?
Excel: = PMT(0.01,420,0,1000000,1)= $153.96
The above two examples are related to ordinary annuity and annuity due.
Example of daily compounding:
- You need $15,000 in 3 years for a new car. If you can deposit money into an account that pays an APR of 5.5% based on daily compounding, how much would you need to deposit?
Excel: =PV(0.00015,1095,0,15000) =$12,718.56
TIMELINE 0 2 3 4 5 7% $100.00 $200.00 -$300.00 $300.00 200*(1.07) = $214.00 100*(1.07)^2 = $114.49 $628.49 Total interest = $628.49-600=28.49 * (1.07)^2 = $ 719.56 Rate Year 1 2 3 7% Nper 2 1 0 CF -100 -200 -300 FV Function $114.49 =FV(0.07,2,0,-100) $214.00 =FV(0.07,1,0,-200) $300.00 =FV(0.07,0,0,-300) Total FV at Year 3 Total FV at Year 5 $628.49 $719.56 =(628.49)*(1.07)^2 (1+r) -1 FV = PMT [(1.075) "" 1 PV = 20000 - 454,513.04 .075Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


